题目内容
已知函数f(x )为奇函数,g(x)=f(x)+1,则g(
)为奇函数,g(x)=f(x)+1,则g( )+
)+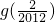 +…+
+…+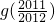 =
=
- A.2012
- B.2011
- C.4020
- D.4022
B
分析:根据题意,可得函数f(x )关于点(0,0)对称,由函数图象的变化规律可得g(x)关于点(
)关于点(0,0)对称,由函数图象的变化规律可得g(x)关于点( ,1)中心对称,进而分析可得g(
,1)中心对称,进而分析可得g( )+g(
)+g( )=2,g(
)=2,g(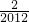 )+g(
)+g(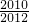 )=2,…g(
)=2,…g(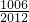 )=g(
)=g( )=1,将各式相加可得答案.
)=1,将各式相加可得答案.
解答:由函数f(x )为奇函数,即函数f(x
)为奇函数,即函数f(x )关于点(0,0)对称,
)关于点(0,0)对称,
则f(x)关于点( ,0)对称,
,0)对称,
又由g(x)=f(x)+1,则g(x)关于点( ,1)中心对称,
,1)中心对称,
则有g( )+g(
)+g( )=2,
)=2,
g(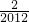 )+g(
)+g(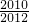 )=2,
)=2,
…
g(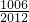 )=g(
)=g( )=1,
)=1,
则g( )+g(
)+g(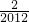 )+…+g(
)+…+g( )=2×1005+1=2011;
)=2×1005+1=2011;
故选B.
点评:本题考查奇偶函数的性质,涉及函数的对称性,关键是根据图象变化的规律,分析得到函数g(x)的对称性.
分析:根据题意,可得函数f(x
 )关于点(0,0)对称,由函数图象的变化规律可得g(x)关于点(
)关于点(0,0)对称,由函数图象的变化规律可得g(x)关于点( ,1)中心对称,进而分析可得g(
,1)中心对称,进而分析可得g( )+g(
)+g( )=2,g(
)=2,g(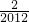 )+g(
)+g(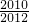 )=2,…g(
)=2,…g(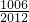 )=g(
)=g( )=1,将各式相加可得答案.
)=1,将各式相加可得答案.解答:由函数f(x
 )为奇函数,即函数f(x
)为奇函数,即函数f(x )关于点(0,0)对称,
)关于点(0,0)对称,则f(x)关于点(
 ,0)对称,
,0)对称,又由g(x)=f(x)+1,则g(x)关于点(
 ,1)中心对称,
,1)中心对称,则有g(
 )+g(
)+g( )=2,
)=2,g(
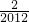 )+g(
)+g(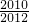 )=2,
)=2,…
g(
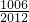 )=g(
)=g( )=1,
)=1,则g(
 )+g(
)+g(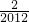 )+…+g(
)+…+g( )=2×1005+1=2011;
)=2×1005+1=2011;故选B.
点评:本题考查奇偶函数的性质,涉及函数的对称性,关键是根据图象变化的规律,分析得到函数g(x)的对称性.

练习册系列答案
相关题目
已知函数f(x)为奇函数,x>0时为增函数且f(2)=0,则{x|f(x-2)>0}=( )
| A、{x|0<x<2或x>4} | B、{x|x<0或x>4} | C、{x|x<0或x>6} | D、{x|x<-2或x>2} |