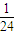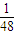题目内容
已知区域A={(x,y)|y≥|x-1|},区域B={(x,y)|y≤2-|x-1|},点P在区域M=A∩B,则|OP|≤1的概率是________.

分析:在直角坐标系中画出区域M=A∩B,以及区域P|OP|≤1,求出区域M的面积,P的面积,通过几何概型求出满足题意的概率.
解答:在直角坐标系中,表示出区域A={(x,y)|y≥|x-1|},
区域B={(x,y)|y≤2-|x-1|},区域M=A∩B,如图中灰色正方形区域,
正方形的边长为:
 ,正方形的面积为:2.
,正方形的面积为:2.点P在区域M内,|OP|≤1,是正方形中红色区域,
它的面积为:
 =
= ,
,所以所求概率是:
 =
= .
.故答案为:
 .
.
点评:本题是以线性规划为载体,考查几何概型的概率的知识,正确理解题意,画出区域M,P,求出面积是解题的关键,考查计算能力.

练习册系列答案
相关题目
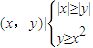 },某人向区域M随机投掷一点P,则点P正好落在区域N的概率为( )
},某人向区域M随机投掷一点P,则点P正好落在区域N的概率为( )