题目内容
下列命题正确的是
- A.若
 ∥
∥ ,且
,且 ∥
∥ ,则
,则 ∥
∥
- B.两个有共同起点且相等的向量,其终点可能不同
- C.向量
 的长度与向量
的长度与向量 的长度相等,且它们是始点、终点相反的向量
的长度相等,且它们是始点、终点相反的向量 - D.若非零向量
 与
与 是共线向量,则A、B、C、D四点共线
是共线向量,则A、B、C、D四点共线
C
分析:用 可验证A不对,由相等向量和相反向量的定义知B不对和C对,由共线向量所在直线的位置关系即平行或重合知D不对.
可验证A不对,由相等向量和相反向量的定义知B不对和C对,由共线向量所在直线的位置关系即平行或重合知D不对.
解答:A、当 =
= 时,由于
时,由于 和任何向量都是共线向量,则
和任何向量都是共线向量,则 与
与 不一定时共线向量,故A不对;
不一定时共线向量,故A不对;
B、由相等向量知,起点相同则终点一定相同,故B不对;
C、由相反向量的定义知,C对;
D、因 ∥
∥ ,则直线AB与直线CD平行或重合,故D不对.
,则直线AB与直线CD平行或重合,故D不对.
故选C.
点评:本题的考点是向量的基本概念,考查了对共线向量、相等向量和相反向量的理解,并且对比了几何中的线线关系,注意特殊情况如 .
.
分析:用
 可验证A不对,由相等向量和相反向量的定义知B不对和C对,由共线向量所在直线的位置关系即平行或重合知D不对.
可验证A不对,由相等向量和相反向量的定义知B不对和C对,由共线向量所在直线的位置关系即平行或重合知D不对.解答:A、当
 =
= 时,由于
时,由于 和任何向量都是共线向量,则
和任何向量都是共线向量,则 与
与 不一定时共线向量,故A不对;
不一定时共线向量,故A不对;B、由相等向量知,起点相同则终点一定相同,故B不对;
C、由相反向量的定义知,C对;
D、因
 ∥
∥ ,则直线AB与直线CD平行或重合,故D不对.
,则直线AB与直线CD平行或重合,故D不对.故选C.
点评:本题的考点是向量的基本概念,考查了对共线向量、相等向量和相反向量的理解,并且对比了几何中的线线关系,注意特殊情况如
 .
. 
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
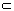 平面β,则下列命题正确的是
平面β,则下列命题正确的是  ,直线b
,直线b 直线a,b
直线a,b 平面
平面 ,则
,则
 则
则 B.若
B.若 , 则
, 则
 则
则 D.若
D.若