题目内容
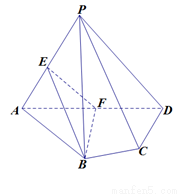
如图,在四棱锥 中,平面PAD⊥平面ABCD,AB=AD,∠BAD=60°,E、F分别是AP、AD的中点
中,平面PAD⊥平面ABCD,AB=AD,∠BAD=60°,E、F分别是AP、AD的中点
求证:(1)直线EF//平面PCD;(2)平面BEF⊥平面PAD

【答案】
(1)因为E、F分别是AP、AD的中点,
 又
又
 直线EF‖平面PCD
直线EF‖平面PCD
(2) F是AD的中点,
F是AD的中点,
又平面PAD⊥平面ABCD,

所以,平面BEF⊥平面PAD。
【解析】略

练习册系列答案
 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案 全优冲刺100分系列答案
全优冲刺100分系列答案
相关题目
 18、如图,在四棱锥P-ABCD中,侧面PAD是正三角形,且与底面ABCD垂直,底面ABCD是边长为2的菱形,∠BAD=60°,N是PB中点,过A、N、D三点的平面交PC于M.
18、如图,在四棱锥P-ABCD中,侧面PAD是正三角形,且与底面ABCD垂直,底面ABCD是边长为2的菱形,∠BAD=60°,N是PB中点,过A、N、D三点的平面交PC于M.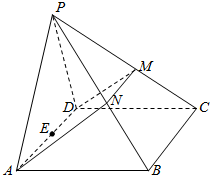 如图,在四棱锥P-ABCD中,侧面PAD是正三角形,且与底面ABCD垂直,底面ABCD是边长为4的菱形,且∠BAD=60°,N是PB的中点,过A,D,N的平面交PC于M,E是AD的中点.
如图,在四棱锥P-ABCD中,侧面PAD是正三角形,且与底面ABCD垂直,底面ABCD是边长为4的菱形,且∠BAD=60°,N是PB的中点,过A,D,N的平面交PC于M,E是AD的中点. 如图,在四棱锥
如图,在四棱锥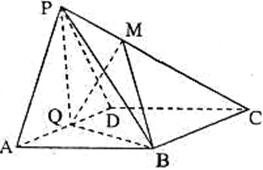 试确定
试确定