题目内容
在等差数列{an}中，若a1+a7+a8+a12=12，则此数列的前13项的和为________．
39
分析：将a1+a7+a8+a12用a1和d表示，再将s13用a1和d表示，从中寻找关系即可解决此数列的前13项的和问题．
解答：设等差数列{an}的公差为d，
∵a1+a7+a8+a12=a1+a1+6d+a1+7d+a1+11d=4a1+24d=12，
∴a1+6d=3，
∴s13=13a1+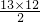
d=13（a1+6d）=39，
故答案为：39．
点评：此题考查学生掌握等差数列的性质，灵活运用等差数列的通项公式及前n项和的公式化简求值，是一道基础题．
分析：将a1+a7+a8+a12用a1和d表示，再将s13用a1和d表示，从中寻找关系即可解决此数列的前13项的和问题．
解答：设等差数列{an}的公差为d，
∵a1+a7+a8+a12=a1+a1+6d+a1+7d+a1+11d=4a1+24d=12，
∴a1+6d=3，
∴s13=13a1+
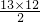d=13（a1+6d）=39，故答案为：39．
点评：此题考查学生掌握等差数列的性质，灵活运用等差数列的通项公式及前n项和的公式化简求值，是一道基础题．
练习册系列答案
励耘书业暑假衔接宁波出版社系列答案
相关题目