题目内容
【题目】设x，y满足约束条件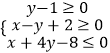 
，且目标函数z=ax+y仅在点（4，1）处取得最大值，则原点O到直线ax﹣y+17=0的距离d的取值范围是（ ）
A.（4 
，17]
B.（0，4 ）
C.（ 
，17]
D.（0， ）
【答案】B
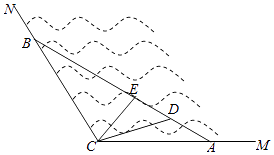
【解析】解：∵约束条件 
作出可行域，如右图可行域，
∵目标函数z=ax+y仅在点A（4，1）取最大值，
当a=0时，z=y仅在y=1上取最大值，不成立；
当a＜0时，目标函数z=ax+y的斜率k=﹣a＞0，
目标函数在（4，1）取不到最大值．
当a＞0时，目标函数z=ax+y的斜率k=﹣a，小于直线x+4y﹣8=0的斜率﹣ 
，∴a＞ ．
综上， ＜a．
原点O到直线ax﹣y+17=0的距离d= 
＜4 
则原点O到直线ax﹣y+17=0的距离d的取值范围是：（0，4 ）
所以答案是：B．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
