题目内容
设数列{an}的前项和为Sn,对任意的n∈N*点(n,
)均在直线y=3x-2上.
(1)求数列{an}的通项公式;
(2)设是数列bn=
,Tn是其前n项和,求使Tn≤
对所有n∈N*都成立的最小正整数m.
| Sn |
| n |
(1)求数列{an}的通项公式;
(2)设是数列bn=
| 3 |
| anan+1 |
| m |
| 20 |
分析:(1)根据对任意的n∈N*点(n,
)均在直线y=3x-2上,可得Sn=3n2-2n,当n≥2时,an=Sn-Sn-1,验证当n=1时,a1=S1,即可求得数列{an}的通项公式;
(2)由(1)知,bn=
=
(
-
),求出和的最小值,即可求得满足要求的最小正整数m.
| Sn |
| n |
(2)由(1)知,bn=
| 3 |
| anan+1 |
| 1 |
| 2 |
| 1 |
| 6n-5 |
| 1 |
| 6n+1 |
解答:解:(1)∵对任意的n∈N*点(n,
)均在直线y=3x-2上.
∴
=3n-2,∴Sn=3n2-2n;
当n≥2时,an=Sn-Sn-1=(3n2-2n)-[3(n-1)2-2(n-1)]=6n-5 ①;
当n=1时,a1=S1=3×12-2=1,适合①式,
所以an=6n-5;
(2)由(1)知,bn=
=
(
-
),
∴Tn=
[(1-
)+(
-
)+…+(
-
)]=
(1-
)
∴
(1-
)≤
对所有n∈N*都成立,只需
≤
∴m≥10
∴满足要求的最小正整数m为10.
| Sn |
| n |
∴
| Sn |
| n |
当n≥2时,an=Sn-Sn-1=(3n2-2n)-[3(n-1)2-2(n-1)]=6n-5 ①;
当n=1时,a1=S1=3×12-2=1,适合①式,
所以an=6n-5;
(2)由(1)知,bn=
| 3 |
| anan+1 |
| 1 |
| 2 |
| 1 |
| 6n-5 |
| 1 |
| 6n+1 |
∴Tn=
| 1 |
| 2 |
| 1 |
| 7 |
| 1 |
| 7 |
| 1 |
| 13 |
| 1 |
| 6n-5 |
| 1 |
| 6n+1 |
| 1 |
| 2 |
| 1 |
| 6n+1 |
∴
| 1 |
| 2 |
| 1 |
| 6n+1 |
| m |
| 20 |
| 1 |
| 2 |
| m |
| 20 |
∴m≥10
∴满足要求的最小正整数m为10.
点评:本题考查了数列与函数的综合应用,用拆项法求数列前n项和以及数列与不等式综合应用问题,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
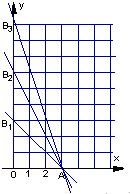 在平面直角坐标系上,设不等式组
在平面直角坐标系上,设不等式组