题目内容
已知等比数列{an}的各项均为不等于1的正数,数列{bn}满足bn=ln an,
b3=18,b6=12,则数列{bn}前n项和的最大值为________.
解析试题分析:由题知 为常数,所以
为常数,所以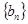 为等差数列
为等差数列 ,
, 解得
解得 ,
, ,由于
,由于 ,因此最大值
,因此最大值 .
.
考点:等差数列的性质和前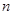 项和公式.
项和公式.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案
相关题目
若 为首项为1的等比数列,
为首项为1的等比数列, 为其前项和,已知
为其前项和,已知 三个数成等差数列,则数列
三个数成等差数列,则数列 的前5项和为( )
的前5项和为( )
| A.341 | B. | C.1023 | D.1024 |
设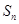 是等差数列
是等差数列 的前n项和,已知
的前n项和,已知 ,
, ,则
,则 等于( )
等于( )
| A.13 | B.35 | C.49 | D.63 |
若等差数列 满足
满足 则
则 ( )
( )
A. | B. | C. | D. |
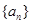 满足
满足 ,则当
,则当 时,
时,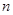 项和最大.
项和最大. 有n条弦的长度成等差数列,最小弦长为数列的首项a1,最大弦长为an,若公差
有n条弦的长度成等差数列,最小弦长为数列的首项a1,最大弦长为an,若公差 ,那么n的可能取值为____ .
,那么n的可能取值为____ . 为等差数列,首项
为等差数列,首项 ,公差
,公差 ,若
,若 成等比数列,且
成等比数列,且 ,
, ,
, ,则
,则 .
. 为等差数列,数列
为等差数列,数列 为等比数列.若
为等比数列.若 ,
, ,且
,且 ,则
,则 的首项为1,其余各项为1或2,且在第
的首项为1,其余各项为1或2,且在第 个1和第
个1和第 个1之间有
个1之间有 个2,即数列
个2,即数列 项和为
项和为 ,则
,则 __ ;
__ ; ___ .
___ .