题目内容
一个袋中装有大小相同的黑球和白球共9个,从中任取2个球,记随机变量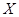 为取出2球中白球的个数,已知
为取出2球中白球的个数,已知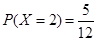 .
.
(Ⅰ)求袋中白球的个数;
(Ⅱ)求随机变量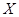 的分布列及其数学期望.
的分布列及其数学期望.
(I)6个;
(II)随机变量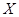 的分布列如下:
的分布列如下: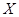
0 1 2 



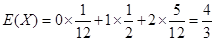
解析试题分析:(I)设袋中有白球n个,利用古典概型的概率计算公式即可得到P(X=2)=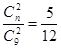 ,解出即可;
,解出即可;
(II)由(I)可知:袋中共有3个黑球,6个白球.随机变量X的取值为0,1,2,利用超几何分布的概率计算公式 可求出相应的概率,即可得出随机变量X的分布列及其数学期望.
可求出相应的概率,即可得出随机变量X的分布列及其数学期望.
试题解析:(Ⅰ)设袋中有白球 个,则
个,则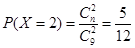 ,
,
即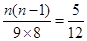 ,解得
,解得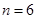 .
.
(Ⅱ)随机变量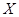 的分布列如下:
的分布列如下: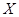
0 1 2 



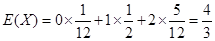
考点:1.古典概型的概率计算公式;2.超几何分布的概率计算公式.

练习册系列答案
 教学练新同步练习系列答案
教学练新同步练习系列答案 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案
相关题目
某校夏令营有3名男同学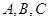 和3名女同学
和3名女同学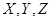 ,其年级情况如下表:
,其年级情况如下表:
| | 一年级 | 二年级 | 三年级 |
| 男同学 |  | 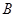 | 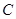 |
| 女同学 | 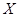 | 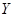 | 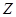 |
现从这6名同学中随机选出2人参加知识竞赛(每人被选到的可能性相同)
(1)用表中字母列举出所有可能的结果
(2)设
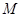 为事件“选出的2人来自不同年级且恰有1名男同学和1名女同学”,求事件
为事件“选出的2人来自不同年级且恰有1名男同学和1名女同学”,求事件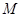 发生的概率.
发生的概率. 为了解某班学生关注NBA是否与性别有关,对本班48人进行了问卷调查得到如下的列联表:
| | 关注NBA | 不关注NBA | 合 计 |
| 男 生 | | 6 | |
| 女 生 | 10 | | |
| 合 计 | | | 48 |
已知在全班48人中随机抽取1人,抽到关注NBA的学生的概率为2/3
⑴请将上面列连表补充完整,并判断是否有
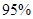 的把握认为关注NBA与性别有关?
的把握认为关注NBA与性别有关?⑵现从女生中抽取2人进一步调查,设其中关注NBA的女生人数为X,求X的分布列与数学期望.
附:
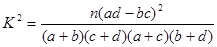 ,其中
,其中 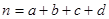
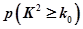 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 |
 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
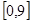 上随机取一实数
上随机取一实数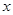 ,则该实数
,则该实数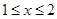 的概率为 .
的概率为 .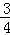 ,求n.
,求n. .已知比赛中,乙先赢了第一局,求:
.已知比赛中,乙先赢了第一局,求: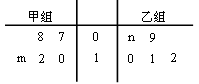
 的值;
的值;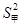 和
和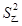 ,
,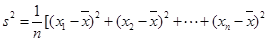 ,
,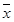 为数据
为数据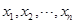 的平均数)
的平均数) 表示取到次品的个数,则E
表示取到次品的个数,则E