题目内容
定义在（﹣∞，0）∪（0，+∞）上的函数f（x），如果对于任意给定的等比数列{an}，{f（an）}仍是等比数列，则称f（x）为“保等比数列函数”．现有定义在（﹣∞，0）∪（0，+∞）上的如下函数：①f（x）=x2；②f（x）=2x；③f（x）=
；④f（x）=ln|x|．则其中是“保等比数列函数”的f（x）的序号为（ ）
|
| A． | ①② | B． | ③④ | C． | ①③ | D． | ②④ |
C解：由等比数列性质知
，①
=f2（an+1），故正确；②
≠
=f2（an+1），故不正确；
③
=
=f2（an+1），故正确；
④f（an）f（an+2）=ln|an|ln|an+2|≠
=f2（an+1），故不正确；故选C
练习册系列答案
相关题目
，
，AP的中点为Q，BQ的中点为R，CR的中点为P，若
，则
，
的前n项和为
，且
，则
的最小值是
C8 D 
成等差数列，则下列不等式一定成立的是（ ）
B.
C.
D.
的公差
且
，则数列
项和
取得最大值时的项数
的定义域为R，当
时，
，且对任意的实数
，
，等式
恒成立.若数列{
}满足
，且
=
，则
的值为 （ ） 
上的偶函数，当
时，
的零点个数为( )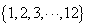
，此集合的符合如下条件的子集的数目为
：子集均含有4个元素，且这4个元素至少有两个是连续的．则