题目内容
设函数 ,m(x)=2lnx..
,m(x)=2lnx..
(1)当p≥1时,证明:对任意x∈(1,+∞),f(x)>m(x)恒成立;
(2)设g(x)=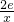 ,若对任意x1,x2∈[1,e],f(x1)-m(x1)<g(x2)成立,求实数p的取值范围.
,若对任意x1,x2∈[1,e],f(x1)-m(x1)<g(x2)成立,求实数p的取值范围.
(1)证明:令G(x)=f(x)-m(x)=px- ,
,
∴ ,
,
即 ,
,
令h(x)=px2-2x+p,
当p≥1时,h(x)=px2-2x+p,
其图象为开口向上的抛物线,
对称轴为
∴h(x)>h(1)=2p-2>0,
∴G'(x)在(1,+∞)内为单调递增函数,
G(x)>G(1)=0,
即f(x)>m(x).
(2)解:∵ 在[1,e]上是减函数,
在[1,e]上是减函数,
∴x=e时,g(x)min=2;x=1时,g(x)max=2e,
即g(x)∈[2,2e].
①当P=0时,h(x)=-2x,
因为x>0,所以h(x)<0, ,
,
∴G(x)在(0,+∞)内是单调递减函数;
②当P<0时,h(x)=px2-2x+p,
其图象为开口向下的抛物线,对称轴为x= ,
,
在(0,+∞),h(x)≤0恒成立,
所以,当p≤0时,G(x)在[1,e]上递减,
G(x)max=G(1)=0<2
③当0<p<1时,由x∈[1,e],
得 ,
,
又当p=1时,G(x)在[1,e]上是增函数,
∴
④当p≥1时,h(x)=px2-2x+p,
其图象为开口向上的抛物线,
对称轴为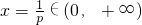 ,
,
∴ ,
,
∴G(x)在[1,e]上为单调递增函数,
又g(x)在[1,e]上是减函数,
故只需G(x)max<g(x)min,x∈[1,e],
而 ,g(x)min=2,
,g(x)min=2,
即 p(e- )-2lne<2,
)-2lne<2,
解得1≤ ,
,
综上,p的取值范围是 .
.
分析:(1)令G(x)=px- ,
, 令h(x)=px2-2x+p,当p≥1时,h(x)=px2-2x+p,其图象为开口向上的抛物线,对称轴为
令h(x)=px2-2x+p,当p≥1时,h(x)=px2-2x+p,其图象为开口向上的抛物线,对称轴为 ,由此能够证明f(x)>m(x).
,由此能够证明f(x)>m(x).
(2)由 在[1,e]上是减函数,知g(x)∈[2,2e].当P=0时,h(x)=-2x,G(x)在(0,+∞)内是单调递减函数;当P<0时,h(x)=px2-2x+p,G(x)max=G(1)=0<2;当0<p<1时,
在[1,e]上是减函数,知g(x)∈[2,2e].当P=0时,h(x)=-2x,G(x)在(0,+∞)内是单调递减函数;当P<0时,h(x)=px2-2x+p,G(x)max=G(1)=0<2;当0<p<1时, ;当p≥1时,
;当p≥1时, .所以G(x)在[1,e]上为单调递增函数,由此能求出p的取值范围.
.所以G(x)在[1,e]上为单调递增函数,由此能求出p的取值范围.
点评:本题考查利用导数求函数的最值及其应用,对数学思维的要求比较高,有一定的探索性.综合性强,难度大,易出错.解题时要认真审题,注意分类讨论思想的灵活运用.
 ,
,∴
 ,
,即
 ,
,令h(x)=px2-2x+p,
当p≥1时,h(x)=px2-2x+p,
其图象为开口向上的抛物线,
对称轴为

∴h(x)>h(1)=2p-2>0,
∴G'(x)在(1,+∞)内为单调递增函数,
G(x)>G(1)=0,
即f(x)>m(x).
(2)解:∵
 在[1,e]上是减函数,
在[1,e]上是减函数,∴x=e时,g(x)min=2;x=1时,g(x)max=2e,
即g(x)∈[2,2e].
①当P=0时,h(x)=-2x,
因为x>0,所以h(x)<0,
 ,
,∴G(x)在(0,+∞)内是单调递减函数;
②当P<0时,h(x)=px2-2x+p,
其图象为开口向下的抛物线,对称轴为x=
 ,
,在(0,+∞),h(x)≤0恒成立,
所以,当p≤0时,G(x)在[1,e]上递减,
G(x)max=G(1)=0<2
③当0<p<1时,由x∈[1,e],
得
 ,
,又当p=1时,G(x)在[1,e]上是增函数,
∴

④当p≥1时,h(x)=px2-2x+p,
其图象为开口向上的抛物线,
对称轴为
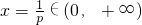 ,
,∴
 ,
,∴G(x)在[1,e]上为单调递增函数,
又g(x)在[1,e]上是减函数,
故只需G(x)max<g(x)min,x∈[1,e],
而
 ,g(x)min=2,
,g(x)min=2,即 p(e-
 )-2lne<2,
)-2lne<2,解得1≤
 ,
,综上,p的取值范围是
 .
.分析:(1)令G(x)=px-
 ,
, 令h(x)=px2-2x+p,当p≥1时,h(x)=px2-2x+p,其图象为开口向上的抛物线,对称轴为
令h(x)=px2-2x+p,当p≥1时,h(x)=px2-2x+p,其图象为开口向上的抛物线,对称轴为 ,由此能够证明f(x)>m(x).
,由此能够证明f(x)>m(x).(2)由
 在[1,e]上是减函数,知g(x)∈[2,2e].当P=0时,h(x)=-2x,G(x)在(0,+∞)内是单调递减函数;当P<0时,h(x)=px2-2x+p,G(x)max=G(1)=0<2;当0<p<1时,
在[1,e]上是减函数,知g(x)∈[2,2e].当P=0时,h(x)=-2x,G(x)在(0,+∞)内是单调递减函数;当P<0时,h(x)=px2-2x+p,G(x)max=G(1)=0<2;当0<p<1时, ;当p≥1时,
;当p≥1时, .所以G(x)在[1,e]上为单调递增函数,由此能求出p的取值范围.
.所以G(x)在[1,e]上为单调递增函数,由此能求出p的取值范围.点评:本题考查利用导数求函数的最值及其应用,对数学思维的要求比较高,有一定的探索性.综合性强,难度大,易出错.解题时要认真审题,注意分类讨论思想的灵活运用.

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案
相关题目
设函数y=f(x)在(a,b)上的导函数为f′(x),f′(x)在(a,b)上的导函数为f″(x),若在a,b)上,f″(x)<0恒成立,则称函数函数f(x)在(a,b)上为“凸函数”.已知当m≤2时,f(x)=
x3-
mx2+x在(-1,2)上是“凸函数”.则f(x)在(-1,2)上( )
| 1 |
| 6 |
| 1 |
| 2 |
| A、既有极大值,也有极小值 |
| B、既有极大值,也有最小值 |
| C、有极大值,没有极小值 |
| D、没有极大值,也没有极小值 |
 ,m(x)=2lnx..
,m(x)=2lnx.. ,若对任意x1,x2∈[1,e],f(x1)-m(x1)<g(x2)成立,求实数p的取值范围.
,若对任意x1,x2∈[1,e],f(x1)-m(x1)<g(x2)成立,求实数p的取值范围.