题目内容
曲线
+
=1上点到直线x-2y+8=0距离的最小值为______.
| x2 |
| 9 |
| y2 |
| 4 |
设椭圆
+
=1上任意一点为P(3cosθ,2sinθ),点P(3cosθ,2sinθ)到直线x-2y+8=0距离为d,
则由点到直线间的距离公式得:
d=
=
(tanφ=
),
∴dmin=
.
∴曲线
+
=1上点到直线x-2y+8=0距离的最小值为
.
故答案为:
.
| x2 |
| 9 |
| y2 |
| 4 |
则由点到直线间的距离公式得:
d=
| |3cosθ-4sinθ+8| | ||
|
| |5cos(θ+φ)+8| | ||
|
| 3 |
| 4 |
∴dmin=
3
| ||
| 5 |
∴曲线
| x2 |
| 9 |
| y2 |
| 4 |
3
| ||
| 5 |
故答案为:
3
| ||
| 5 |

练习册系列答案
相关题目
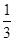 ACAE=
ACAE= AB,BD,CE相交于点F.
AB,BD,CE相交于点F.
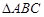 内接于⊙
内接于⊙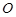 ,
, 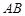 是⊙
是⊙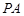 是过点
是过点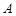 的直线, 且
的直线, 且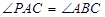 .
.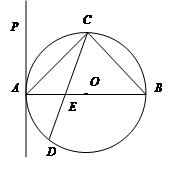
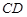 交
交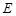 ,
, 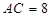 ,
, 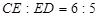 ,
, 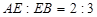 , 求
, 求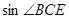 .
.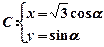 (
(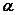 为参数); 直线
为参数); 直线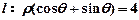 .
.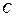 的普通方程和直线l的直角坐标方程;
的普通方程和直线l的直角坐标方程; 的参数方程为
的参数方程为 ,
, 对应的参数是
对应的参数是 ,则点
,则点 之间的距离是( )
之间的距离是( )



 ,则直线的斜率为( )
,则直线的斜率为( )


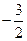
 ,且
,且 ,
, 一定不通过第 象限.
一定不通过第 象限.