题目内容
若a>2,则函数f(x)=x3-ax2+1在区间(0,2)上恰好有( )
| A.0个零点 | B.1个零点 | C.2个零点 | D.3个零点 |
B
先根据导数判断出函数f(x)在区间[0,2]上单调递减,再由f(0)f(2)<0可知有唯一零点.
解:由已知得:f′(x)=x(x-2a),由于a>2,
故当0<x<2时f′(x)<0,
即函数为区间(0,2)上的单调递减函数,
又当a>2时
f(0)f(2)= -4a<0,
-4a<0,
故据二分法及单调性可知函数在区间(0,2)上有且只有一个零点.
故选B
解:由已知得:f′(x)=x(x-2a),由于a>2,
故当0<x<2时f′(x)<0,
即函数为区间(0,2)上的单调递减函数,
又当a>2时
f(0)f(2)=
 -4a<0,
-4a<0,故据二分法及单调性可知函数在区间(0,2)上有且只有一个零点.
故选B

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
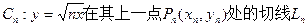 总经过定点(
总经过定点( ,0)
,0) 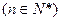
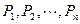 在同一直线上
在同一直线上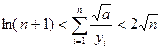
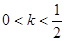 时,方程
时,方程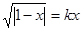 的解的个数是
的解的个数是 节性服装当季节即将来临时,价格呈上升趋势,设某服装开始时定价为10元,并且每周(7天)涨价2元,5周后开始保持20元的价格平稳销售;10周后当季节即将过去时,平均每周削价2元,直到16周末,该服装已不再销售.
节性服装当季节即将来临时,价格呈上升趋势,设某服装开始时定价为10元,并且每周(7天)涨价2元,5周后开始保持20元的价格平稳销售;10周后当季节即将过去时,平均每周削价2元,直到16周末,该服装已不再销售.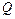 与周次t之间的关系为
与周次t之间的关系为 ,
,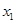 是方程
是方程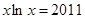 的根,
的根,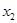 是方程
是方程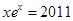 的根,则下列关于
的根,则下列关于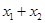 B.
B. 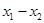 C.
C. 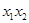 D.
D. 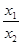
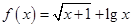 的定义域是 ( )
的定义域是 ( )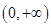
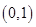
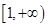
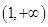
 、
、 两座城市相距100千米,现计划在这两座城市之间修筑一条高等级公路(即线段
两座城市相距100千米,现计划在这两座城市之间修筑一条高等级公路(即线段 )。经测量,森林保护区中心
)。经测量,森林保护区中心 点在
点在 的背面靠墙的矩形小屋,房屋
的背面靠墙的矩形小屋,房屋 正面的造价为1200元/
正面的造价为1200元/ 元,如果墙面高为3m,且不计房屋背面费用,问怎样设计房屋能使得总造价最低,最低造价为多少元?
元,如果墙面高为3m,且不计房屋背面费用,问怎样设计房屋能使得总造价最低,最低造价为多少元?
 b
b