题目内容
（2012•广东模拟）已知|
|=|
|=|
-
|=2，则|
-
|的值为
| a |
| b |
| a |
| b |
| 2a |
| b |
2
| 3 |
2
．| 3 |
分析：根据题意，分析可得
与
的夹角为60°，由数量积的定义，计算可得
•
的值，则|2
-
|2=4
2-4
•
+
2，代入数据可得|2
-
|2的值，开方可得答案．
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| a |
| b |
| b |
| a |
| b |
解答：
解：根据题意，设
=
，
=
，则
-
=
-
=
，如图
|
|=|
|=|
-
|=2，则△AOB为等边三角形，
则
与
的夹角为60°，有
•
=|
|•|
|cos60•=2，
则|2
-
|2=4
2-4
•
+
2=12，
|2
-
|=
=2
，
故答案为2
．
解：根据题意，设| OA |
| a |
| OB |
| b |
| a |
| b |
| OA |
| OB |
| BA |
|
| a |
| b |
| a |
| b |
则
| a |
| b |
| a |
| b |
| a |
| b |
则|2
| a |
| b |
| a |
| a |
| b |
| b |
|2
| a |
| b |
| 12 |
| 3 |
故答案为2
| 3 |
点评：本题考查平面向量数量积的运算，本题的关键分析得到
与
的夹角．
| a |
| b |
练习册系列答案
相关题目
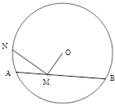（2012•广东模拟）（几何证明选讲选做题）如图，点M为⊙O的弦AB上的一点，连接MO．MN⊥OM，MN交圆于N，若MA=2，MB=4，则MN=