题目内容
(本题满分10分)已知圆 :
: ,直线
,直线 过定点
过定点

(1)若直线 与圆相切,切点为
与圆相切,切点为 ,求线段
,求线段 的长度;
的长度;
(2)若 与圆相交于
与圆相交于 两点,线段
两点,线段 的中点为
的中点为 ,又
,又 与
与 :
: 的交点为
的交点为 ,判断
,判断
 是否为定值,若是,则求出定值;若不是,请说明理由
是否为定值,若是,则求出定值;若不是,请说明理由
(1)
(2)
【解析】
试题分析:(1)由 可求得
可求得 .(2)先判断
.(2)先判断 斜率存在,然后设其方程为
斜率存在,然后设其方程为 ,求出点
,求出点 ,再由
,再由 解得
解得 ,通过运算可得
,通过运算可得 ,故
,故
 是定值.
是定值.
试题解析:(1) ,所以切线长
,所以切线长 (4分)
(4分)
(2)易知,若斜率不存在,则 与圆相切,
与圆相切,
若斜率为0,则 与圆相离,故直线的斜率存在,
与圆相离,故直线的斜率存在,
可设 的方程:
的方程: 由
由 解得
解得 ,再由
,再由 解得
解得 ,又直线
,又直线 ,
, 解得
解得
所以 为定值(也可以用几何法证明)(10分)
为定值(也可以用几何法证明)(10分)
考点:直线与圆的位置关系.
考点分析: 考点1:直线和圆的位置关系 试题属性- 题型:
- 难度:
- 考核:
- 年级:

练习册系列答案
相关题目
 ,
, ,
, ,...,以此类推,第5个等式为( )
,...,以此类推,第5个等式为( )



 ,则
,则 的值为( )
的值为( ) B、
B、 C、
C、 D、
D、
 ,则
,则 = .
= . ;
; ,直线
,直线 将△
将△ 分割为面积相等的两部分,则
分割为面积相等的两部分,则 ( )
( ) B.
B. C.
C. D.
D. 
 上一点
上一点 到
到 轴的距离为4,则
轴的距离为4,则 点到该抛物线焦点的距离为 .
点到该抛物线焦点的距离为 .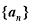 是一个单调递增的等差数列,且满足
是一个单调递增的等差数列,且满足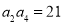 ,
,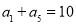 ,数列
,数列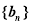 的前
的前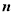 项和为
项和为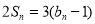
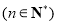 .
.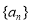 的通项公式;(Ⅱ)证明数列
的通项公式;(Ⅱ)证明数列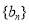 是等比数列.
是等比数列.