题目内容
函数
的单调减区间为________．
（3，+∞）
分析：利用复合函数单调性，在定义域范围内求出u=（x+1）（x-3）单增区间 即可．
解答：由（x+1）（x-3）＞0得函数定义域为A=（-∞，-1）∪（3，+∞），∵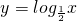
在（0，+∞）上单调递减，
所以原函数的单调减区间即为u=（x+1）（x-3）在A上的单增区间，即为（3，+∞）
故答案为：（3，+∞）
点评：本题考查复合函数的单调性．用到了指数函数、二次函数的单调性．务必注意单调区间是定义域的子集，首先考虑定义域．
分析：利用复合函数单调性，在定义域范围内求出u=（x+1）（x-3）单增区间 即可．
解答：由（x+1）（x-3）＞0得函数定义域为A=（-∞，-1）∪（3，+∞），∵
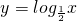在（0，+∞）上单调递减，所以原函数的单调减区间即为u=（x+1）（x-3）在A上的单增区间，即为（3，+∞）
故答案为：（3，+∞）
点评：本题考查复合函数的单调性．用到了指数函数、二次函数的单调性．务必注意单调区间是定义域的子集，首先考虑定义域．
练习册系列答案
相关题目
如图，三次函数y=ax3+bx2+cx+d的零点为-1，1，2，则该函数的单调减区间为
的单调减区间为
（B）
（C）
（D） 