题目内容
若函数f(x)=-tx2+2x+1(t<0,t为常数),对于任意两个不同的x1,x2,当x1,x2∈[-2,2]时,均有|f(x1)-f(x2)|≤k|x1-x2|( k为常数,k∈R)成立,如果满足条件的最小正整数k等于4,则实数t的取值范围是分析:f(x1)-f(x2)|≤k|x1-x2|( k为常数,k∈R)成立,变为|-t(x1+x2)+2|≤k当x1,x2∈[-2,2]时,恒成立,如果满足条件的最小正整数k等于4得到|-t(x1+x2)+2|≤4,当x1,x2∈[-2,2]时,恒成立,求出t的范围即可.
解答:解:根由题意f(x)=-tx2+2x+1(t<0,t为常数),对于任意两个不同的x1,x2,均有|f(x1)-f(x2)|≤k|x1-x2|( k为常数,k∈R)成立,
∴|-t(x1+x2)+2|≤k当x1,x2∈[-2,2]时,恒成立,
∵x1,x2∈[-2,2],任意两个不同的x1,x2,t<0
∴-t(x1+x2)+2∈(4t+2,-4t+2)
∴|-t(x1+x2)+2|∈[0,-4t+2)
∴-4t+2<k
∵满足条件的最小正整数k等于4,
∴-4t+2<4
∴t>-
,
∵t<0,t为常数
∴-
<t<0
故答案为(-
,0)
∴|-t(x1+x2)+2|≤k当x1,x2∈[-2,2]时,恒成立,
∵x1,x2∈[-2,2],任意两个不同的x1,x2,t<0
∴-t(x1+x2)+2∈(4t+2,-4t+2)
∴|-t(x1+x2)+2|∈[0,-4t+2)
∴-4t+2<k
∵满足条件的最小正整数k等于4,
∴-4t+2<4
∴t>-
| 1 |
| 2 |
∵t<0,t为常数
∴-
| 1 |
| 2 |
故答案为(-
| 1 |
| 2 |
点评:考查学生函数与方程的综合运用能力,以及理解不等式恒成立条件的能力.

练习册系列答案
相关题目
 时,判断函数f(x)=
时,判断函数f(x)=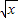 是否属于集合C∩D?并说明理由.若是,则求出区间[a,b];
是否属于集合C∩D?并说明理由.若是,则求出区间[a,b]; 0时,若函数f(x)=
0时,若函数f(x)=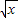 +t∈C∩D,求实数t的取值范围;
+t∈C∩D,求实数t的取值范围;