题目内容
下列四个函数中,既是定义域上的奇函数又在区间 内单调递增的是( )
内单调递增的是( )
A. | B. | C. | D. |
B
解析试题分析:根据题意,由于A. 不具有奇偶性,定义域不关于原点对称,对于 B.
不具有奇偶性,定义域不关于原点对称,对于 B. 是奇函数,在
是奇函数,在 内是增函数,成立对于C.
内是增函数,成立对于C. ,是奇函数,但是不满足递增性,对于 D.
,是奇函数,但是不满足递增性,对于 D. ,是奇函数,不满足在
,是奇函数,不满足在 递增,故可知答案为B.
递增,故可知答案为B.
考点:函数的单调性
点评:主要是考查了函数奇偶性以及单调性的运用,属于基础题。

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
在平面直角坐标系中,横坐标和纵坐标均为整数的点称为格点,如果函数 的图象恰好通过
的图象恰好通过 个格点,则称函数
个格点,则称函数 为
为 阶格点函数. 给出下列4个函数:
阶格点函数. 给出下列4个函数:
① ;②
;② ;③
;③ ;④
;④ .
.
其中是一阶格点函数的是 ( )
| A.①③ | B.②③ | C.③④ | D.①④ |
设定义在 上的函数
上的函数 满足
满足 若
若 ,则
,则 ( )
( )
| A.13 | B.2 | C. | D. |
方程 有唯一解,则实数
有唯一解,则实数 的取值范围是( )
的取值范围是( )
A. | B. |
C. 或 或 | D. 或 或 或 或 |
下列函数中,周期是 且在
且在 上为增函数的是( )
上为增函数的是( )
A. | B. | C. | D. |
函数 的图象如图所示,则
的图象如图所示,则 的解析式可能是 ( )
的解析式可能是 ( ) 
A. | B. |
C. | D. |
若函数 在
在 是增函数,则a的取值范围是( )
是增函数,则a的取值范围是( )
A. | B. | C. | D. |
 和
和 ,动点
,动点 在直线
在直线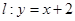 上移动,椭圆
上移动,椭圆 以
以 为焦点且经过点
为焦点且经过点 ,记椭圆
,记椭圆 ,则函数
,则函数 的大致图像( )
的大致图像( )
 的图象大致为( )
的图象大致为( )