题目内容
对于函数y=f（x）和其定义域的子集D，若存在常数M，使得对于任意的x1∈D，存在唯一的x2∈D，满足等式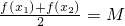
，则称M为f（x）在D上的均值．下列函数中以
为其在（0，+∞）上的唯一均值的是________（填所有你认为符合条件的函数的序号）①
； ②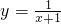
； ③y=-x2+1； ④y=log2x．
②④
分析：首先分析题目求对于任意的x1∈D，存在唯一的x2∈D，使
成立的函数．
对于函数①，可直接取任意的x1∈R，验证即可；
对于函数②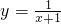，可直接取任意的x1∈R，验证求出唯一的 x2=4-x1，即可得到成立．故②对．
对于函数③y=-x2+1，特殊值法代入验证不成立成立．即可得到答案．
对于函数④y=log2x，定义域为x＞0，值域为R且单调，显然成立．
解答：对于函数①；定义域为R，值域为y＞0．对于x1=-1，f（x1）=2．要使 
成立，则f（x2）=-1，不成立．
对于函数②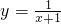，可直接取任意的x1∈R，验证求出唯一的 x2=
，即可得到成立．故②对．
对于函数③y=-x2+1，取任意的x1∈R，
=，
，可以两个的x2∈D．故不满足条件．
对于函数④y=log2x，定义域为x＞0，值域为R且单调，显然必存在唯一的x2∈D，使成立．故成立．
故答案为：②④
点评：此题主要应用新定义的方式考查平均值不等式在函数中的应用．对于新定义的问题，需要认真分析定义内容，切记不可偏离题目．
分析：首先分析题目求对于任意的x1∈D，存在唯一的x2∈D，使
成立的函数．对于函数①
，可直接取任意的x1∈R，验证即可；对于函数②
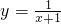，可直接取任意的x1∈R，验证求出唯一的 x2=4-x1，即可得到成立．故②对．对于函数③y=-x2+1，特殊值法代入验证不成立成立．即可得到答案．
对于函数④y=log2x，定义域为x＞0，值域为R且单调，显然成立．
解答：对于函数①
；定义域为R，值域为y＞0．对于x1=-1，f（x1）=2．要使 成立，则f（x2）=-1，不成立．对于函数②
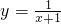，可直接取任意的x1∈R，验证求出唯一的 x2=，即可得到成立．故②对．对于函数③y=-x2+1，取任意的x1∈R，
=，，可以两个的x2∈D．故不满足条件．对于函数④y=log2x，定义域为x＞0，值域为R且单调，显然必存在唯一的x2∈D，使
成立．故成立．故答案为：②④
点评：此题主要应用新定义的方式考查平均值不等式在函数中的应用．对于新定义的问题，需要认真分析定义内容，切记不可偏离题目．
练习册系列答案
星级口算天天练系列答案
相关题目