题目内容
(2012•湛江二模)(坐标系与参数方程选做题)在平面直角坐标系xOy中,直线l的参数方程为
(参数t∈R),圆的参数方程为
(参数θ∈[0,2π)),则圆心到直线l的距离为
|
|
2
| 2 |
2
.| 2 |
分析:先将直线和圆的参数方程化为普通方程,再利用点到直线的距离公式求出圆心到直线l的距离
解答:直线l的参数方程为
(参数t∈R),消去t得普通方程为x+y-6=0,
圆的参数方程为
,消去θ得出,x2+(y-2)2=4,表示以(0,2)为圆心,以2为半径的圆.
根据点到直线的距离公式,圆心到直线l的距离d=
=2
故答案为:2
|
圆的参数方程为
|
根据点到直线的距离公式,圆心到直线l的距离d=
| |2-6| | ||
|
| 2 |
故答案为:2
| 2 |
点评:本题从极坐标与直角坐标的转化出发,考查了点到直线的距离公式的应用.属于基础题.

练习册系列答案
相关题目
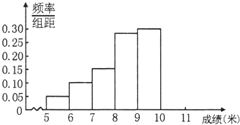 (2012•湛江二模)某市为了解今年高中毕业生的身体素质状况,从本市某校高中毕业班中抽取一个班进行实心球测试,成绩在8米及以上的为合格.把所得数据进行整理后,分成6组画出频率分布直方图的一部分(如图),已知第一小组为[5,6),从左到右前5个小组的频率分别为0.06,0.10,0.14,0.28,0.30.第6小组的频数是6.
(2012•湛江二模)某市为了解今年高中毕业生的身体素质状况,从本市某校高中毕业班中抽取一个班进行实心球测试,成绩在8米及以上的为合格.把所得数据进行整理后,分成6组画出频率分布直方图的一部分(如图),已知第一小组为[5,6),从左到右前5个小组的频率分别为0.06,0.10,0.14,0.28,0.30.第6小组的频数是6. (2012•湛江二模)运行如图所示框图,坐标满足不等式组
(2012•湛江二模)运行如图所示框图,坐标满足不等式组 (2012•湛江二模)如图,Rt△ABC中,∠C=90°,∠A=30°,圆O经过B、C且与AB、AC分别相交于D、E.若AE=EC=
(2012•湛江二模)如图,Rt△ABC中,∠C=90°,∠A=30°,圆O经过B、C且与AB、AC分别相交于D、E.若AE=EC=