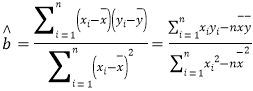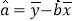题目内容
【题目】已知![]()
(1)求曲线![]() 在点
在点![]() 出的切线方程;
出的切线方程;
(2)设函数![]() ,若不等式
,若不等式![]() 对
对![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】分析:(1)求出![]() ,由
,由![]() 的值可得切点坐标,求出
的值可得切点坐标,求出![]() 的值,可得切线斜率,利用点斜式可得曲线
的值,可得切线斜率,利用点斜式可得曲线![]() 在点
在点![]() 处的切线方程;(2)
处的切线方程;(2)![]() ,等价于
,等价于![]() ,
,![]() ,
,![]() ,利用导数研究函数的单调性,可得要满足
,利用导数研究函数的单调性,可得要满足![]() 对
对![]() 恒成立,只需
恒成立,只需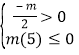 ,从而可得结果.
,从而可得结果.
详解:(1)由题知:![]() ,则
,则![]() ,
,
∴曲线在点![]() 处切线的斜率为
处切线的斜率为![]()
所以,切线方程为![]() ,即
,即![]() .
.
(2)由题知:![]() ,即
,即![]() ,
,
令![]() ,则
,则![]() ,
,
令![]() 解得
解得![]() ,
,
∴![]() 在
在![]() 单增;
单增;![]() 单减,
单减,
又∵![]() 有唯一零点
有唯一零点![]()
所以,可作出函数![]() 的示意图,
的示意图,
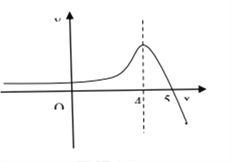
要满足![]() 对
对![]() 恒成立,只需
恒成立,只需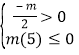 解得
解得![]() .即实数
.即实数![]() 的取值范围是
的取值范围是![]()
法二:令![]() ,则
,则![]() ,
,
令![]() ,则
,则![]() , 令
, 令![]() ,则
,则![]() ,
,
∴![]() 在
在![]() 单增,
单增,![]() 单减;
单减;![]() ,故
,故![]() 对
对![]() 恒成立.
恒成立.
∴![]() 在
在![]() 单减,
单减,
又∵![]() 对
对![]() 恒成立,令
恒成立,令![]() 得
得![]()
∴![]() ,无论
,无论![]() 在
在![]() 有无零点,
有无零点,
∴![]() 在
在![]() 上的最小值只可能为
上的最小值只可能为![]() 或
或![]() ,
,
要![]() 恒成立,
恒成立,
∴![]() 且
且![]() ,
,
∴![]() .即实数
.即实数![]() 的取值范围是
的取值范围是![]()

练习册系列答案
相关题目
【题目】在一次抽样调查中测得样本的5个样本点,数值如下表:
| 0.25 | 0.5 | 1 | 2 | 4 |
| 16 | 12 | 5 | 2 | 1 |
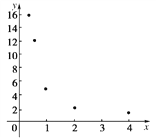
(1)根据散点图判断,![]() 哪一个适宜作为
哪一个适宜作为![]() 关于
关于![]() 的回归方程类型?(给出判断即可,不必说明理由)
的回归方程类型?(给出判断即可,不必说明理由)
(2)根据(1)的判断结果试建立![]() 与
与![]() 之间的回归方程.(注意
之间的回归方程.(注意![]() 或
或![]() 计算结果保留整数)
计算结果保留整数)
(3)由(2)中所得设z=![]() +
+![]() 且
且![]() ,试求z的最小值。
,试求z的最小值。
参考数据及公式如下:
![]() ,
,![]() ,
,