题目内容
已知等比数列{an}的首项a1=2,公比q=3,Sn是它的前n项和,求证: 。
。
 。
。证明:由已知,得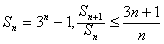 等价于
等价于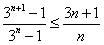 ,
,
即3n≥2n+1,(*)
用数学归纳法证明.
①当n=1时,左边=3,右边=3,所以(*)成立;
②假设当n=k时,(*)成立,即3k≥2k+1,
那么当n=k+1时,3k+1=3×3k≥3(2k+1)=6k+3≥2k+3=2(k+1)+1,
所以当n=k+1时,(*)成立,
综合①②,得3n≥2n+1成立,
所以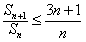 。
。
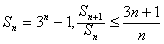 等价于
等价于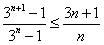 ,
,即3n≥2n+1,(*)
用数学归纳法证明.
①当n=1时,左边=3,右边=3,所以(*)成立;
②假设当n=k时,(*)成立,即3k≥2k+1,
那么当n=k+1时,3k+1=3×3k≥3(2k+1)=6k+3≥2k+3=2(k+1)+1,
所以当n=k+1时,(*)成立,
综合①②,得3n≥2n+1成立,
所以
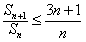 。
。 
练习册系列答案
相关题目