题目内容
已知函数f(x)=4cosxsin(x- )+
)+ .
.
(1)求函数f(x)在区间[ ,
, ]上的值域;
]上的值域;
(2)在△ABC中,角A,B,C,所对的边分别是a,b,c,若角C为锐角,f(C)= ,且c=2,求△ABC面积的最大值.
,且c=2,求△ABC面积的最大值.
解:(1)f(x)=4cosxsin(x- )+
)+ =sin2x-
=sin2x- cos2x=2sin(2x-
cos2x=2sin(2x- ),…4分
),…4分
由 ≤x≤
≤x≤ ,有
,有 ≤2x-
≤2x- ≤
≤ ,∴得函数f(x)的值域为[1,2].…6分
,∴得函数f(x)的值域为[1,2].…6分
(2)由f(C)= ,有sin(2C-
,有sin(2C- )=
)= ,
,
∵C为锐角,∴2C- =
= ,∴C=
,∴C= .…9分
.…9分
∵c=2,∴由余弦定理得:a2+b2-ab=4,
∵a2+b2≥2ab,∴4=a2+b2-ab≥ab.
∴S△ABC=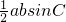 =
=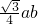 ≤
≤ ,
,
∴当a=b,即△ABC为正三角形时,△ABC的面积有最大值 .…13分.
.…13分.
分析:(1)利用差角的正弦公式、辅助角公式化简函数,结合正弦函数的性质,可得函数f(x)在区间[ ,
, ]上的值域;
]上的值域;
(2)先求出C,再利用余弦定理,结合基本不等式,即可求得△ABC面积的最大值.
点评:本题考查三角函数的化简,考查三角函数的性质,考查三角形面积的计算,考查基本不等式的运用,属于中档题.
 )+
)+ =sin2x-
=sin2x- cos2x=2sin(2x-
cos2x=2sin(2x- ),…4分
),…4分由
 ≤x≤
≤x≤ ,有
,有 ≤2x-
≤2x- ≤
≤ ,∴得函数f(x)的值域为[1,2].…6分
,∴得函数f(x)的值域为[1,2].…6分(2)由f(C)=
 ,有sin(2C-
,有sin(2C- )=
)= ,
,∵C为锐角,∴2C-
 =
= ,∴C=
,∴C= .…9分
.…9分∵c=2,∴由余弦定理得:a2+b2-ab=4,
∵a2+b2≥2ab,∴4=a2+b2-ab≥ab.
∴S△ABC=
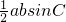 =
=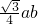 ≤
≤ ,
,∴当a=b,即△ABC为正三角形时,△ABC的面积有最大值
 .…13分.
.…13分.分析:(1)利用差角的正弦公式、辅助角公式化简函数,结合正弦函数的性质,可得函数f(x)在区间[
 ,
, ]上的值域;
]上的值域;(2)先求出C,再利用余弦定理,结合基本不等式,即可求得△ABC面积的最大值.
点评:本题考查三角函数的化简,考查三角函数的性质,考查三角形面积的计算,考查基本不等式的运用,属于中档题.

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目