题目内容
正三棱柱ABC-A1B1C1的各条棱长均为3,长为2的线段MN的一个端点M在AA1上运动,另一端点N在底面ABC上运动,则MN的中点P的轨迹(曲面)与正三棱柱共顶点A的三个面所围成的几何体的体积为________.

分析:由题设中的条件可以判断出MN的中点P的轨迹(曲面)与正三棱柱共顶点A的三个面所围成的几何体是一个半径为1的球的一部分,故由球的体积公式求即可
解答:由题意知,∠MAN=90°,再由P是中点,知AP=
 MN=1,故MN的中点P的轨迹(曲面)是一个球面的一部分,此球以A球心,1为半径
MN=1,故MN的中点P的轨迹(曲面)是一个球面的一部分,此球以A球心,1为半径由题意MN的中点P的轨迹(曲面)与正三棱柱共顶点A的三个面所围成的几何体此球的体积的

故其体积为
 =
=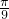
故答案为
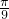
点评:本题考查球的体积与表面积,解题的关键是根据题中的条件确定出所围成的几何体是一个球的一部分且能根据正三棱柱的几何特征及此几何体的几何特征出其体积正好是相应球的体积的
 ,本题考查了空间想像能力.
,本题考查了空间想像能力. 
练习册系列答案
 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案 新思维寒假作业系列答案
新思维寒假作业系列答案
相关题目
 如图:在正三棱柱ABC-A1 B1 C1中,AB=
如图:在正三棱柱ABC-A1 B1 C1中,AB= 如图在 正三棱柱ABC-A1 B1 C1中,底面边长为
如图在 正三棱柱ABC-A1 B1 C1中,底面边长为 如图,在正三棱柱ABC-A1 B1 C1中,AA1=4,AB=2,M是AC的中点,点N在AA1上,AN=
如图,在正三棱柱ABC-A1 B1 C1中,AA1=4,AB=2,M是AC的中点,点N在AA1上,AN= 如图:在正三棱柱ABC-A1 B1 C1中,AB=
如图:在正三棱柱ABC-A1 B1 C1中,AB= =a,E,F分别是BB1,CC1上的点且BE=a,CF=2a.
=a,E,F分别是BB1,CC1上的点且BE=a,CF=2a. =a,E,F分别是BB1,CC1上的点且BE=a,CF=2a.
=a,E,F分别是BB1,CC1上的点且BE=a,CF=2a.