题目内容
（不等式选讲选做题）不等式|x2-3x-4|＞x+1的解集是
{x|x＞5或x＜-1或-1＜x＜3}
{x|x＞5或x＜-1或-1＜x＜3}
．分析：原不等式等价于（Ⅰ）
或（Ⅱ）
，分别求出（Ⅰ）和（Ⅱ）的解集，取并集即得所求．
|
|
解答：解：原不等式等价于（Ⅰ）
或（Ⅱ）
，
等价于
或
，等价于x＞5或x＜-1或-1＜x＜3．
∴原不等式的解集为{x|x＞5或x＜-1或-1＜x＜3}．
故答案为 {x|x＞5或x＜-1或-1＜x＜3}．
|
|
等价于
|
|
∴原不等式的解集为{x|x＞5或x＜-1或-1＜x＜3}．
故答案为 {x|x＞5或x＜-1或-1＜x＜3}．
点评：本题主要考查一元二次不等式、绝对值不等式的解法，体现了等价转化的数学思想，属于中档题．
练习册系列答案
怎样学好牛津英语系列答案
相关题目
，则线段CD的长为 ．
）的直角坐标是 ．
，则线段CD的长为 ．
）的直角坐标是 ．
，则线段CD的长为 ．
）的直角坐标是 ．
，则线段CD的长为 ．
）的直角坐标是 ．
，则线段CD的长为 ．
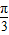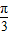）的直角坐标是 ．