题目内容
15、如果存在实数x使不等式|x+1|-|x-2|＜k成立，则实数k的取值范围是
k＞-3
．分析：利用表示数轴上的 x到-1的距离减去它到2的距离，它|的最小值等于-3，而且存在实数x使不等式|x+1|-|x-2|＜k成立，
可得k＞-3．
可得k＞-3．
解答：解：∵存在实数x使不等式|x+1|-|x-2|＜k成立，|x+1|-|x-2|表示数轴上的 x到-1的距离减去它到2的距离，
最小值等于-3，故 k＞-3，
故答案为：k＞-3．
最小值等于-3，故 k＞-3，
故答案为：k＞-3．
点评：本题考查绝对值不等式的解法，绝对值的意义，求出|x+1|-|x-2|的最小值是解题的关键．
练习册系列答案
53随堂测系列答案
相关题目
A．（不等式选讲选做题）如果存在实数x使不等式|x+1|-|x-2|＜k成立，则实数k的取值范围是
A．（不等式选讲选做题）如果存在实数x使不等式|x+1|-|x-2|＜k成立，则实数k的取值范围是________．
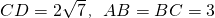，则AC的长为________．
，则AC的长为 ．