题目内容
若定义在正整数有序对集合上的二元函数f满足:
①f(x,x)=x,②f(x,y)=f(y,x),③(x+y)·f(x,y)=y·f(x,x+y),则f(12,16)的值是________.
48
解析 由③(x+y)·f(x,y)=y·f(x,x+y),易得
f(x,x+y)=![]() ·f(x,y).结合①②,得
·f(x,y).结合①②,得
f(12,16)=f(12,12+4)=![]() f(12,4)=4f(4,12)
f(12,4)=4f(4,12)
=4f(4,4+8)=4·![]() ·f(4,8)=6·f(4,4+4)
·f(4,8)=6·f(4,4+4)
=6·![]() ·f(4,4)=
·f(4,4)=![]() 12f(4,4)=12×4=48.
12f(4,4)=12×4=48.

练习册系列答案
相关题目
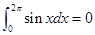 ;
;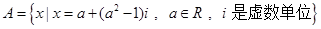 ,若
,若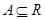 ,则
,则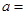 1
1 为定义在R上的可导函数,且
为定义在R上的可导函数,且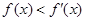 对于
对于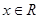 恒成立,则有
恒成立,则有 ,
, 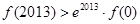 ;
;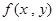 满足:(1)
满足:(1)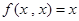 ,(2)
,(2)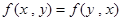 (3)
(3)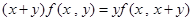 ,则
,则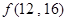 =
=
 ;
; ,若
,若 ,则
,则 1
1 为定义在R上的可导函数,且
为定义在R上的可导函数,且 对于
对于 恒成立,则有
恒成立,则有 ,
,  ;
; 满足:(1)
满足:(1) ,(2)
,(2) (3)
(3) ,则
,则 =
=