题目内容
【题目】函数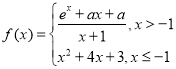 ,则关于x的方程
,则关于x的方程![]() 的实数解最多有( )
的实数解最多有( )
A.7个B.10个C.12个D.15个
【答案】C
【解析】
判断![]() 的单调性,作出
的单调性,作出![]() 的大致函数图象,求出
的大致函数图象,求出![]() 的解,再根据
的解,再根据![]() 的图象得出
的图象得出![]() 的解得个数即可得出结论.
的解得个数即可得出结论.
当![]() 时,
时,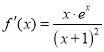
∴![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增.
上单调递增.
∴当![]() 时,
时,![]() 取得极小值
取得极小值![]() .
.
当![]() 时,由二次函数性质可知
时,由二次函数性质可知![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,
上单调递增,
∴当![]() 时,
时,![]() 取得极小值
取得极小值![]() .
.
当![]() 时,则
时,则![]() 有4个解,不妨设从小到大依次为
有4个解,不妨设从小到大依次为![]() ,
,
则![]() ,
,![]() ,
,![]() .
.
再令![]() ,作出
,作出![]() 的函数图象如图所示:
的函数图象如图所示:
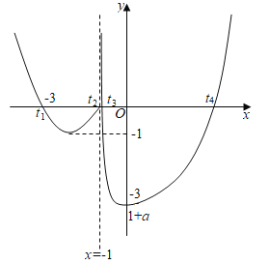
![]() ,则
,则![]() ,(
,(![]() =1,2,3,4).
=1,2,3,4).
由图象可知![]() 有2解,
有2解,![]() 有3解,
有3解,![]() 有4解,
有4解,![]() 有3解,
有3解,
此时![]() 有12解.
有12解.
当![]() 时,则
时,则![]() 有4个解,
有4个解,![]()
则![]() 有3解,
有3解,![]() 至多3解,
至多3解,![]() 至多1解,
至多1解,![]() 至多4解.
至多4解.
此时方程![]() 至多11解.
至多11解.
当![]() 时,则
时,则![]() 有2个解,
有2个解,![]() ,
,
由上可知![]() 无实数根,
无实数根,![]() 有1解,所以
有1解,所以![]() 有1解.
有1解.
当![]() 时,则
时,则![]() 有3个解,
有3个解,![]() ,
,
由上可知![]() 无实数根,
无实数根,![]() 有1解,
有1解, ![]() 有4解.
有4解.
所以此时![]() 有5解.
有5解.
综上所述:![]() 至多12解.
至多12解.
故选:C.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目