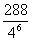题目内容
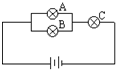 如图中灯泡A,B,C是否正常是相互独立的,它们不亮的概率分别是0.1,0.2,0.1.
如图中灯泡A,B,C是否正常是相互独立的,它们不亮的概率分别是0.1,0.2,0.1.(Ⅰ)求所有灯泡都亮的概率;
(Ⅱ)求有灯泡亮也有灯泡不亮的概率.
分析:(Ⅰ)由于灯泡A,B,C是否正常是相互独立的,所有灯泡都亮的概率是三个灯泡亮的概率的乘积,记事件A1、A2、A3分别表示灯泡A、B、C不亮,所有灯泡都亮的概率为P(
•
•
)=P(
)•P(
)•P(
),代入数据计算即可得到答案
(II)事件“有灯泡亮也有灯泡不亮”说明整个电路是通的,有灯光不亮只能是A,B两者之一不亮,C必须亮,故事件“有灯泡亮也有灯泡不亮”概率是P(
A2A3+A1
A3)=P(
A2A3)+P(A1
A3)代入数据计算即可得到有灯泡亮也有灯泡不亮的概率
. |
| A1 |
. |
| A2 |
. |
| A3 |
. |
| A1 |
. |
| A2 |
. |
| A3 |
(II)事件“有灯泡亮也有灯泡不亮”说明整个电路是通的,有灯光不亮只能是A,B两者之一不亮,C必须亮,故事件“有灯泡亮也有灯泡不亮”概率是P(
. |
| A1 |
. |
| A2 |
. |
| A1 |
. |
| A2 |
解答:解:(I)记事件A1、A2、A3分别表示灯泡A、B、C不亮,它们相互独立,则所有灯泡都亮的概率为:
P(
•
•
)=P(
)•P(
)•P(
)=(1-0.1)×(1-0.2)×(1-0.1)=0.648
答:所有灯泡都亮的概率是0.648
(II)A、B中有一只亮,一只不亮,C必须亮,即求概率为
P(
A2A3+A1
A3)=P(
A2A3)+P(A1
A3)
=0.1×(1-0.2)×(1-0.1)+(1-0.1)×0.2×(1-0.1)=0.234
答:有灯泡亮也有灯泡不亮的概率是0.234
P(
. |
| A1 |
. |
| A2 |
. |
| A3 |
. |
| A1 |
. |
| A2 |
. |
| A3 |
答:所有灯泡都亮的概率是0.648
(II)A、B中有一只亮,一只不亮,C必须亮,即求概率为
P(
. |
| A1 |
. |
| A2 |
. |
| A1 |
. |
| A2 |
=0.1×(1-0.2)×(1-0.1)+(1-0.1)×0.2×(1-0.1)=0.234
答:有灯泡亮也有灯泡不亮的概率是0.234
点评:本题考查相互独立事件的概率乘法公式,互斥事件和事件的概率,解题的关键是理解两个事件,找到对应的概率模型,利用公式求出它们的概率,本题考查了转化的思想及判断推理的能力,是概率在物理中的应用,有着实际背景的概率题是近几年高考的命题方向,平时要注意积累此类题抽象出概率模型的方法

练习册系列答案
 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案
相关题目

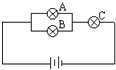 如图中灯泡A,B,C是否正常是相互独立的,它们不亮的概率分别是0.1,0.2,0.1.
如图中灯泡A,B,C是否正常是相互独立的,它们不亮的概率分别是0.1,0.2,0.1.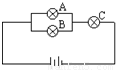
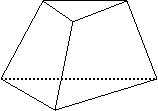 A.
A.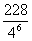 B.
B.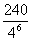 C.
C.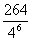 D.
D.