题目内容
设双曲线C: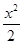 -y2=1的左、右顶点分别为A1、A2,垂直于x轴的直线m与双曲线C交于不同的两点P、Q.
-y2=1的左、右顶点分别为A1、A2,垂直于x轴的直线m与双曲线C交于不同的两点P、Q.
(1)若直线m与x轴正半轴的交点为T,且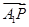 ·
·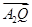 =1,求点T的坐标;
=1,求点T的坐标;
(2)求直线A1P与直线A2Q的交点M的轨迹E的方程;
(3)过点F(1,0)作直线l与(2)中的轨迹E交于不同的两点A、B,设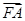 =λ·
=λ·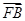 ,若λ∈[-2,-1],求|
,若λ∈[-2,-1],求|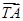 +
+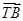 |(T为(1)中的点)的取值范围.
|(T为(1)中的点)的取值范围.
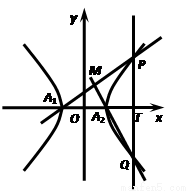
(1)(2,0)(2)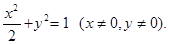 (3)
(3)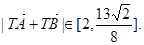
【解析】(1)由双曲线方程可得A1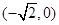 , A2
, A2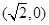 ,设直线m的方程为x=a,代入椭圆方程求出P,Q的坐标,再根据
,设直线m的方程为x=a,代入椭圆方程求出P,Q的坐标,再根据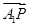 ·
·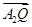 =1建立关于a的方程,求出a值,从而求出T点坐标.
=1建立关于a的方程,求出a值,从而求出T点坐标.
(2)设出直线m:x=a,然后求出P、Q的坐标,再求出直线A1P与直线A2Q方程,从而解方程组求出交点M的参数方程,消去参数a之后即可得到点M的轨迹E的普通方程.
(3)容易验证直线l的斜率不为0.故可设直线l的方程为 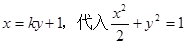 中,得
中,得 ,再根据韦达定理可得y1,y2与k的两个关系式,再根据
,再根据韦达定理可得y1,y2与k的两个关系式,再根据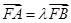 得到
得到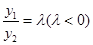 ,从而可知
,从而可知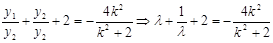
问题互此转化为关于k的函数来解决即可.
解:(1)由题,得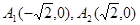 ,设
,设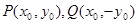
则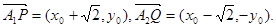
由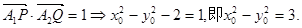 …………①
…………①
又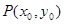 在双曲线上,则
在双曲线上,则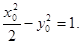 …………②
…………②
联立①、②,解得 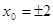 由题意,
由题意, 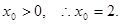
∴点T的坐标为(2,0) …………3分
(2)设直线A1P与直线A2Q的交点M的坐标为(x,y)
由A1、P、M三点共线,得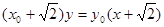 …………③
…………③
由A2、Q、M三点共线,得 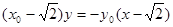 …………④
…………④
联立③、④,解得
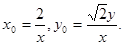 ∵
∵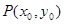 在双曲线上,
在双曲线上,
∴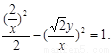 ∴轨迹E的方程为
∴轨迹E的方程为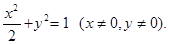 …………8分
…………8分
(3)容易验证直线l的斜率不为0.故可设直线l的方程为 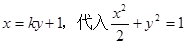 中,得
中,得 设
设 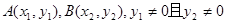
则由根与系数的关系,得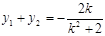 ……⑤
……⑤ 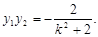 ……⑥
……⑥
∵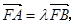 ∴有
∴有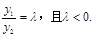 将⑤式平方除以⑥式,得
将⑤式平方除以⑥式,得
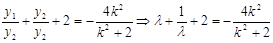 由
由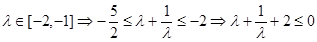
 ………………10分
………………10分
∵
又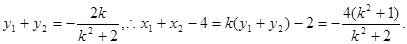
故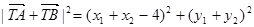 ……………….12分
……………….12分
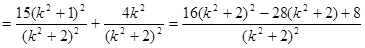
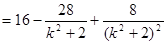 令
令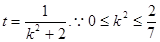 ∴
∴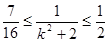 ,即
,即 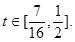 ∴
∴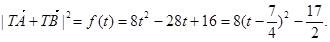
而 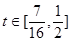 , ∴
, ∴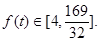
∴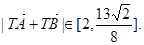 …………………….14分
…………………….14分

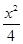 -y2=1的右焦点为F,直线l过点F且斜率为k,若直线l与双曲线C的左、右两支都相交,则直线l的斜率的取值范围是
-y2=1的右焦点为F,直线l过点F且斜率为k,若直线l与双曲线C的左、右两支都相交,则直线l的斜率的取值范围是
 或k≥
或k≥