题目内容
已知函数 ,那么下列命题中假命题是( )
,那么下列命题中假命题是( )
A. 既不是奇函数,也不是偶函数 既不是奇函数,也不是偶函数 | B. 在 在 上恰有一个零点 上恰有一个零点 |
C. 是周期函数 是周期函数 | D. 在 在 上是增函数 上是增函数 |
B
解析试题分析:∵f(x)=cos2x+sinx,∴f(-x)=cos2x-sinx,故f(x)既不是奇函数也不是偶函数,即A是真命题;∵由f(x)=cos2x+sinx=1-sin2x+sinx=0,得sinx= ,∴f(x)在[-π,0]上恰有2个零点,即B是假命题;∵f(x)=cos2x+sinx=1-sin2x+sinx=-(sinx-
,∴f(x)在[-π,0]上恰有2个零点,即B是假命题;∵f(x)=cos2x+sinx=1-sin2x+sinx=-(sinx- )2+
)2+ ,∴f(x)是周期函数,即C是真命题;∵f(x)=cos2x+sinx=1-sin2x+sinx=-(sinx-
,∴f(x)是周期函数,即C是真命题;∵f(x)=cos2x+sinx=1-sin2x+sinx=-(sinx- )2+
)2+ ,∴f(x)在
,∴f(x)在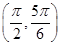 上是增函数,即D是真命题.故选B.
上是增函数,即D是真命题.故选B.
考点:本题考查了三角函数的性质及命题的真假判断
点评:解此类试题时要注意三角函数恒等变换及性质的灵活运用,属基础题

练习册系列答案
 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案
相关题目
已知函数
 的图象如图所示,则
的图象如图所示,则 等于
等于
A. | B. | C. | D. |
已知函数y=2sin(ωx+φ)(ω>0)在区间[0,2π]的图像如下:那么ω=( )
| A.1 | B.2 |
| C.1/2 | D.1/3 |
若 则 ( )
则 ( )
A. | B. |
C. | D. |
已知sin ,则sin
,则sin
A. | B. | C. | D.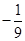 |
将函数 的图象向左平移
的图象向左平移 后得到函数
后得到函数 ,则
,则 具有性质( )
具有性质( )
A.最大值为 ,图象关于直线 ,图象关于直线 对称 对称 | B.周期为 ,图象关于 ,图象关于 对称 对称 |
C.在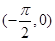 上单调递增,为偶函数 上单调递增,为偶函数 | D.在 上单调递增,不为奇函数 上单调递增,不为奇函数 |
 ,
,
 B
B  C
C 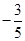 D
D 
 是实数,则函数
是实数,则函数 的图像可能是 ( )
的图像可能是 ( )
 (
( 且
且 )的图象为 ( )
)的图象为 ( )