题目内容
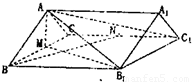
如图:已知四棱柱ABCD—A1B1C1D1的底面是正方形,O1、O分别是上、下底面的中心,A1O⊥平面ABCD. (1)求证:平面O1DC⊥平面ABCD; (2)若点E在棱AA1上,且AE=2EA1,
问在棱BC上是否存在点F,使得EF⊥BC?若存在,求出其位置;若不存在,说明理由.
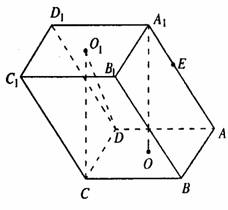
证明:(1)连结AC、BD、A1C1则AC、BD的交点,O1为
|
![]()
∴四边形ACC1A1为平行四边形,
∴四边形A1O1CO为平行四边形…………2分
∴A1O//CO1
∵A1O⊥平面ABCD
∴O1C⊥平面ABCD…………………………4分
∵O1C![]() 平面O1DC
平面O1DC
∴存在点平面O1DC⊥平面ABCD……………5分
(2)F为BC的三等分点B(靠近B)时,有EF⊥BC……………………6分
过点E作EH⊥AC于H,连FH、EF//A1O
∵平面A1AO⊥平面ABCD
∴EH⊥平面ABCD
又BC![]() 平面ABCD ∴BC⊥EH ①
平面ABCD ∴BC⊥EH ①
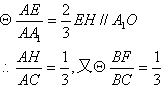
∴HF//AB ∴HF⊥BC, ②
由①②知,BC⊥平面EFH∵EF![]() 平面EFH ∴EF⊥BC…………………………12分
平面EFH ∴EF⊥BC…………………………12分

练习册系列答案
 快乐5加2金卷系列答案
快乐5加2金卷系列答案
相关题目
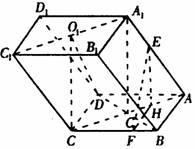
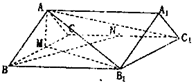 如图,已知直棱柱ABC-A1B1C1中,AB=AC=5,BC=BB1=8,M,N分别为棱BC,CC1的中点.
如图,已知直棱柱ABC-A1B1C1中,AB=AC=5,BC=BB1=8,M,N分别为棱BC,CC1的中点. (2007•无锡二模)如图,已知四棱柱ABCD-A1B1C1D1的底面ABCD为直角梯形,AB∥CD,AB⊥AD,AB=AD=A1B=2CD,侧面A1ADD1为正方形.
(2007•无锡二模)如图,已知四棱柱ABCD-A1B1C1D1的底面ABCD为直角梯形,AB∥CD,AB⊥AD,AB=AD=A1B=2CD,侧面A1ADD1为正方形.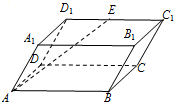 如图,已知四棱柱ABCD-A1B1C1D1的底面ABCD是矩形,AB=4,AA1=3,∠BAA1=60°,E为棱C1D1的中点,则
如图,已知四棱柱ABCD-A1B1C1D1的底面ABCD是矩形,AB=4,AA1=3,∠BAA1=60°,E为棱C1D1的中点,则