题目内容
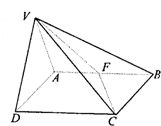 如图,平面VAD⊥平面ABCD,△VAD是等边三角形,ABCD是矩形,AB:AD=
如图,平面VAD⊥平面ABCD,△VAD是等边三角形,ABCD是矩形,AB:AD=| 2 |
(1)求VC与平面ABCD所成的角;
(2)求二面角V-FC-B的度数;
(3)当V到平面ABCD的距离是3时,求B到平面VFC的距离.
分析:(1)取AD的中点G,连接VG,CG.由△ADV为正三角形,知VG⊥AD.由平面VAD⊥平面ABCD.AD为交线,知VG⊥平面ABCD,则∠VCG为CV与平面ABCD所成的角.由此能求出VC与平面ABCD所成的角的大小.
(2)连接GF,则GF=
=
a.而FC=
=
a.在△GFC中,GC2=GF2+FC2.所以GF⊥FC.连接VF,由VG⊥平面ABCD知VF⊥FC,则∠VFG即为二面角V-FC-D的平面角.由此能求出二面角V-FC-B的度数.
(3)设B到平面VFC的距离为h,当V到平面ABCD的距离是3时,即VG=3.此时AD=BC=2
,FB=
,FC=3
,VF=3
.所以S△VFC=
VF•FC=9,S△BFC=
FB•BC=3
.由VV-FCB=VB-VCF,能求出B到面VCF的距离.
(2)连接GF,则GF=
| AG2+AF2 |
| ||
| 2 |
| FB2+BC2 |
| ||
| 2 |
(3)设B到平面VFC的距离为h,当V到平面ABCD的距离是3时,即VG=3.此时AD=BC=2
| 3 |
| 6 |
| 2 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
解答: 解:取AD的中点G,连接VG,CG.
解:取AD的中点G,连接VG,CG.
(1)∵△ADV为正三角形,∴VG⊥AD.
又平面VAD⊥平面ABCD.AD为交线,
∴VG⊥平面ABCD,
则∠VCG为CV与平面ABCD所成的角.
设AD=a,则VG=
a,DC=
a.
在Rt△GDC中,GC=
=
=
a.
在Rt△VGC中,tan∠VCG=
=
.
∴∠VCG=30°.
即VC与平面ABCD成30°.
(2)连接GF,则GF=
=
a.
而 FC=
=
a.
在△GFC中,GC2=GF2+FC2.
∴GF⊥FC.
连接VF,由VG⊥平面ABCD知VF⊥FC,
则∠VFG即为二面角V-FC-D的平面角.
在Rt△VFG中,VG=GF=
a.
∴∠VFG=45°.
故二面角V-FC-B的度数为135°.
(3)设B到平面VFC的距离为h,当V到平面ABCD的距离是3时,
即VG=3.
此时AD=BC=2
,FB=
,FC=3
,VF=3
.
∴S△VFC=
VF•FC=9,
S△BFC=
FB•BC=3
.
∵VV-FCB=VB-VCF,
∴
•VG•S△FBC=
•h•S△VFC.
∴
×3×3
=
•h•9.
∴h=
,即B到面VCF的距离为
.
 解:取AD的中点G,连接VG,CG.
解:取AD的中点G,连接VG,CG.(1)∵△ADV为正三角形,∴VG⊥AD.
又平面VAD⊥平面ABCD.AD为交线,
∴VG⊥平面ABCD,
则∠VCG为CV与平面ABCD所成的角.
设AD=a,则VG=
| ||
| 2 |
| 2 |
在Rt△GDC中,GC=
| DC2+GD2 |
2a2+
|
| 3 |
| 2 |
在Rt△VGC中,tan∠VCG=
| VG |
| GC |
| ||
| 3 |
∴∠VCG=30°.
即VC与平面ABCD成30°.
(2)连接GF,则GF=
| AG2+AF2 |
| ||
| 2 |
而 FC=
| FB2+BC2 |
| ||
| 2 |
在△GFC中,GC2=GF2+FC2.
∴GF⊥FC.
连接VF,由VG⊥平面ABCD知VF⊥FC,
则∠VFG即为二面角V-FC-D的平面角.
在Rt△VFG中,VG=GF=
| ||
| 2 |
∴∠VFG=45°.
故二面角V-FC-B的度数为135°.
(3)设B到平面VFC的距离为h,当V到平面ABCD的距离是3时,
即VG=3.
此时AD=BC=2
| 3 |
| 6 |
| 2 |
| 2 |
∴S△VFC=
| 1 |
| 2 |
S△BFC=
| 1 |
| 2 |
| 2 |
∵VV-FCB=VB-VCF,
∴
| 1 |
| 3 |
| 1 |
| 3 |
∴
| 1 |
| 3 |
| 2 |
| 1 |
| 3 |
∴h=
| 2 |
| 2 |
点评:本题考查直线与平面所成的角的求法,求二面角的度数求点到平面的距离.考查运算求解能力,推理论证能力;考查化归与转化思想.综合性强,难度大,易出错,是高考的重点.解题时要认真审题,仔细解答.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 11、如图所示,平面M、N互相垂直,棱l上有两点A、B,AC?M,BD?N,且AC⊥l,AB=8cm,AC=6cm,BD=24cm,则CD=
11、如图所示,平面M、N互相垂直,棱l上有两点A、B,AC?M,BD?N,且AC⊥l,AB=8cm,AC=6cm,BD=24cm,则CD= 如图,边长为a的正△ABC的中线AF与中位线DE相交于G,已知△A′ED是△AED绕DE旋转过程中的一个图形,现给出下列命题,其中正确的命题有
如图,边长为a的正△ABC的中线AF与中位线DE相交于G,已知△A′ED是△AED绕DE旋转过程中的一个图形,现给出下列命题,其中正确的命题有 (2012•石景山区一模)如图,已知平面α∩β=l,A、B是l上的两个点,C、D在平面β内,且DA⊥α,CB⊥α,AD=4,AB=6,BC=8,在平面α上有一个动点P,使得∠APD=∠BPC,则△PAB面积的最大值是( )
(2012•石景山区一模)如图,已知平面α∩β=l,A、B是l上的两个点,C、D在平面β内,且DA⊥α,CB⊥α,AD=4,AB=6,BC=8,在平面α上有一个动点P,使得∠APD=∠BPC,则△PAB面积的最大值是( )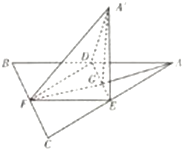 如图,边长为a的等边三角形ABC的中线AF与中位线DE交于点G,将△ADE绕DE旋转得到△A′DE(A′∉平面ABC),则下列叙述错误的是( )
如图,边长为a的等边三角形ABC的中线AF与中位线DE交于点G,将△ADE绕DE旋转得到△A′DE(A′∉平面ABC),则下列叙述错误的是( )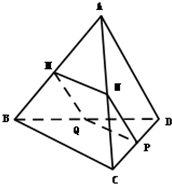 如图,在三棱锥A-BCD中,平行于BC的平面MNPQ分别交AB、AC、CD、BD于M、N、P、Q四点,且MN=PQ.
如图,在三棱锥A-BCD中,平行于BC的平面MNPQ分别交AB、AC、CD、BD于M、N、P、Q四点,且MN=PQ.