题目内容
已知向量
，且
，则锐角a为（ ）A．30°
B．60°
C．45°
D．75°
【答案】分析：利用两个向量共线的性质可得 x1y2-x2y1=0，再利用二倍角的正弦公式求得sina=
，从而求得锐角a 的值．
解答：解：∵
，
∴x1y2-x2y1=0，即
-sin
•cos
=0，
解得sina=
，故锐角a=30°，
故选A．
点评：本题主要考查两个向量共线的性质，二倍角的正弦公式的应用，根据三角函数的值求角，属于中档题．
，从而求得锐角a 的值．解答：解：∵
，∴x1y2-x2y1=0，即
-sin•cos=0，解得sina=
，故锐角a=30°，故选A．
点评：本题主要考查两个向量共线的性质，二倍角的正弦公式的应用，根据三角函数的值求角，属于中档题．
练习册系列答案
培优好卷单元加期末卷系列答案
一线名师权威作业本系列答案
相关题目
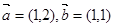，且
与
的夹角为锐角，则实数
的取值范围是______.
，且
与
共线，则锐角
等于
b
且向量a与向量b的夹角为锐角，则
的取值范围是
． 
，且
，则锐角a为