题目内容
圆 与圆
与圆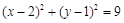 的位置关系为( )
的位置关系为( )
| A.内切 | B.相交 | C.外切 | D.相离 |

解析试题分析:两圆的圆心为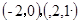 ,半径分别为2,3.所以圆心距为
,半径分别为2,3.所以圆心距为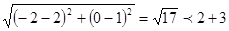 ,所以两圆相交.
,所以两圆相交.
考点:两圆位置关系的判断.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
设P是圆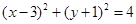 上的动点,Q是直线
上的动点,Q是直线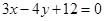 上的动点,则
上的动点,则 的最小值为( )
的最小值为( )
| A.1 | B.2 | C.3 | D.4 |
若实数x,y满足: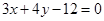 ,则
,则 的最小值是( )
的最小值是( )
| A.2 | B.3 | C.5 | D.8 |
已知函数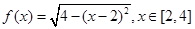 对于满足
对于满足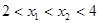 的任意
的任意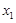 ,
,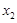 ,给出下列结论:
,给出下列结论:
①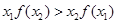
②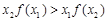
③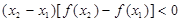
④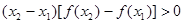
其中正确的是( )
| A.①③ | B.①④ | C.②③ | D.②④ |
已知圆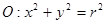 ,点
,点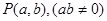 是圆
是圆 内的一点,过点
内的一点,过点 的圆
的圆 的最短弦在直线
的最短弦在直线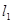 上,直线
上,直线 的方程为
的方程为 ,那么( )
,那么( )
A.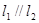 且 且 与圆 与圆 相交 相交 | B. 且 且 与圆 与圆 相切 相切 |
C.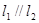 且 且 与圆 与圆 相离 相离 | D. 且 且 与圆 与圆 相离 相离 |
已知圆C1:(x-2)2+(y-3)2=1,圆C2:(x-3)2+(y-4)2=9,M,N分别是圆C1,C2上的动点,P为x轴上的动点,则|PM|+|PN|的最小值为( )
A.5 -4 -4 | B.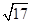 -1 -1 |
C.6-2 | D.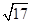 |
若圆x2+y2-2kx+2y+2=0(k>0)与两坐标轴无公共点,那么实数k的取值范围为( )
| A.-1<k<1 | B.1<k<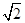 |
| C.1<k<2 | D.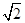 <k<2 <k<2 |
若原点在圆(x-m)2+(y+m)2=8的内部,则实数m的取值范围是( )
A.-2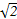 <m<2 <m<2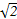 | B.0<m<2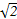 |
| C.-2<m<2 | D.0<m<2 |
已知圆(x-a)2+(y-b)2=r2的圆心为抛物线y2=4x的焦点,且与直线3x+4y+2=0相切,则该圆的方程为( ).
A.(x-1)2+y2= | B.x2+(y-1)2= |
| C.(x-1)2+y2=1 | D.x2+(y-1)2=1 |