题目内容
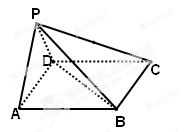
如图,在多面体ABCDE中,DB⊥平面ABC,AE∥DB,且△ABC是边长为2的等边三角形,AE=1,CD与平面ABDE所成角的正弦值为 .
.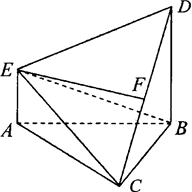
(Ⅰ)若F是线段CD的中点,证明:EF⊥面DBC;
(Ⅱ)求二面角D-EC-B的平面角的余弦值.
(Ⅰ)详见解析;(Ⅱ)二面角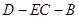 的平面角的余弦值为
的平面角的余弦值为 .
.
解析试题分析:(Ⅰ)此题关键是建立空间坐标系,需要找三条两两垂直的直线,注意到△ABC是边长为2的等边三角形,可考虑取AB的中点O,则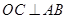 ,取BD的中点为G,则
,取BD的中点为G,则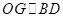 ,从而得到三条两两垂直的直线,这样就可以建立空间坐标系,根据题中条件,求出个点坐标,要证明
,从而得到三条两两垂直的直线,这样就可以建立空间坐标系,根据题中条件,求出个点坐标,要证明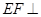 面
面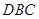 ,只需证
,只需证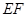 平行平面
平行平面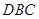 的一个法向量即可,此题也可以用传统方法来解;(Ⅱ)求二面角D-EC-B的平面角的余弦值,只需找出平面的一个法向量,利用法向量来求即可,值得注意的是,需要判断二面角是钝角还是锐角,否则求出的值不对.
的一个法向量即可,此题也可以用传统方法来解;(Ⅱ)求二面角D-EC-B的平面角的余弦值,只需找出平面的一个法向量,利用法向量来求即可,值得注意的是,需要判断二面角是钝角还是锐角,否则求出的值不对.
试题解析:(Ⅰ)证明:取AB的中点O,连结OC,OD,则 ,
,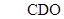 即是
即是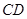 与平面
与平面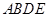 所成角,
所成角,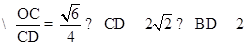 ,取BD的中点为G,以
,取BD的中点为G,以 为原点,
为原点, 为
为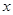 轴,
轴, 为
为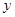 轴,
轴, 为
为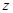 轴建立如图空间直角坐标系,则
轴建立如图空间直角坐标系,则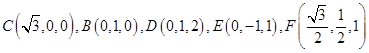 ,取BC的中点为M,则
,取BC的中点为M,则 面
面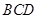
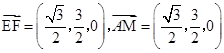 ,所以
,所以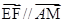 ,所以
,所以 面
面 ;
;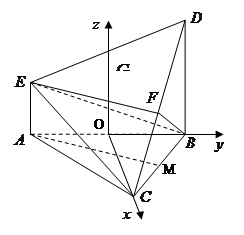
(Ⅱ)解:由上面知: ,又
,又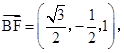 取平面DEC的一个法向量
取平面DEC的一个法向量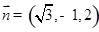 ,又
,又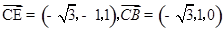 ,设平面BCE的一个法向量
,设平面BCE的一个法向量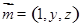 ,由
,由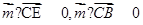 ,由此得平面BCE的一个法向量
,由此得平面BCE的一个法向量 则
则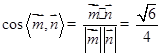 ,所以二面角
,所以二面角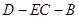 的平面角的余弦值为
的平面角的余弦值为 .
.
考点:本小题考查线面垂直的判定以及二面角的求法,考查学生的化归与转化能力以及空间想象能力,

练习册系列答案
相关题目
 ,平面PAC⊥平面ABC,PD⊥AC于点D,AD=1,CD=3,PD=
,平面PAC⊥平面ABC,PD⊥AC于点D,AD=1,CD=3,PD= .
.
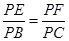 =λ.
=λ.
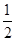 时,求异面直线BF与CD所成角的余弦值;
时,求异面直线BF与CD所成角的余弦值;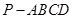 中,底面
中,底面 是边长为
是边长为 的正方形,侧面
的正方形,侧面
 底面
底面 .
.
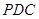 ;
; 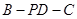 的余弦值.
的余弦值.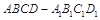 ,中,
,中,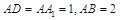 ,点
,点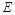 在棱AB上移动.
在棱AB上移动.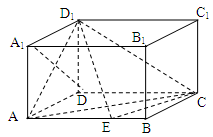
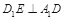 ;
; 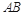 的中点时,求点
的中点时,求点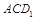 的距离;
的距离; 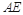 等于何值时,二面角
等于何值时,二面角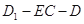 的大小为
的大小为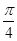 .
.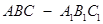 中,△
中,△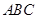 是边长为
是边长为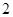 的等边三角形,
的等边三角形, 平面
平面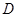 ,
,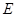 分别是
分别是 ,
,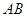 的中点.
的中点. 
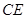 ∥平面
∥平面 ;
;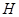 为
为 上的动点,当
上的动点,当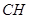 与平面
与平面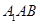 所成最大角的正切值为
所成最大角的正切值为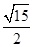 时,求平面
时,求平面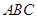 的底边
的底边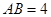 ,点
,点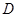 在线段
在线段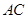 上,
上,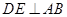 于
于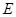 ,现将
,现将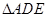 沿
沿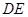 折起到
折起到 的位置(如图(2)).
的位置(如图(2)).
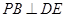 ;
;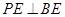 ,直线
,直线 与平面
与平面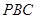 所成的角为
所成的角为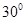 ,求
,求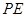 长.
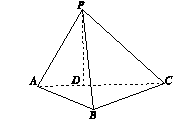
长.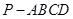 中,顶点
中,顶点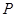 在底面
在底面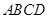 内的射影恰好落在
内的射影恰好落在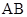 的中点
的中点 上,又
上,又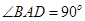 ,
,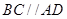 且
且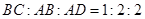
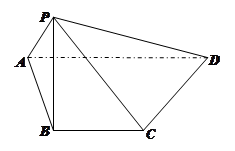
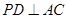 ;
;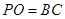 ,求直线
,求直线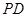 与
与 所成角的余弦值;
所成角的余弦值;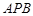 与平面
与平面 所成的角为
所成的角为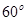 ,求
,求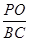 的值。
的值。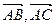 为一组邻边的平行四边形的面积S;
为一组邻边的平行四边形的面积S;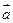 分别与向量
分别与向量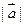 =
= ,求向量
,求向量