题目内容
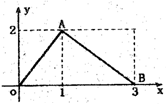 函数f(x)的图象是如图所示的折线段OAB,点A坐标为(1,2),点B坐标为(3,0),定义函数g(x)=f(x)•x,则函数g(x)最大值为
函数f(x)的图象是如图所示的折线段OAB,点A坐标为(1,2),点B坐标为(3,0),定义函数g(x)=f(x)•x,则函数g(x)最大值为| 9 |
| 4 |
| 9 |
| 4 |
分析:先根据函数f(x)的图象求出解析式,再根据g(x)=f(x)•x求的函数g(x)的解析式,结合函数g(x)的解析式即可求的函数g(x)最大值.
解答:解:由题意知:函数f(x)的解析式为:f(x)=
,
又∵g(x)=f(x)•x.
∴函数g(x)的解析式为:g(x)=
当0≤x≤1时,g(x)=2x2,∴gmax(x)=g(1)=2;
当1<x≤3时,g(x)=-(x-
)2+
>2.
∴函数g(x)最大值为
.
故答案为:
.
|
又∵g(x)=f(x)•x.
∴函数g(x)的解析式为:g(x)=
|
当0≤x≤1时,g(x)=2x2,∴gmax(x)=g(1)=2;
当1<x≤3时,g(x)=-(x-
| 3 |
| 2 |
| 9 |
| 4 |
∴函数g(x)最大值为
| 9 |
| 4 |
故答案为:
| 9 |
| 4 |
点评:本题主要考查了分段函数解析式的求法和分段函数求最值的综合问题,同时考查了分类讨论的数学思想,属于中档题.

练习册系列答案
相关题目
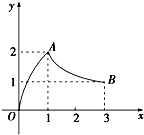
如图,函数f(x)的图象是曲线OAB,则f(
)的值等于( )
| 1 |
| f(3) |

| A、1 | B、2 | C、3 | D、0 |