题目内容
(本小题满分12分)
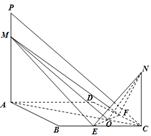
如图,已知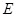 ,
,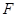 分别是正方形
分别是正方形 边
边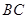 、
、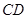 的中点,
的中点,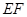 与
与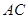 交于点
交于点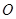 ,
,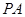 、
、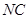 都垂直于平面
都垂直于平面 ,且
,且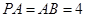 ,
,
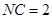 ,
,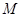 是线段
是线段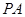 上一动点.
上一动点.
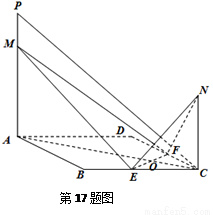
(Ⅰ)求证:平面 平面
平面 ;
;
(Ⅱ)试确定点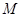 的位置,使得
的位置,使得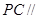 平面
平面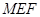 ;
;
(Ⅲ)当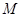 是
是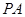 中点时,求二面角
中点时,求二面角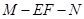 的余弦值.
的余弦值.
【答案】
(Ⅰ)见解析;(Ⅱ)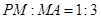 ;(Ⅲ)
;(Ⅲ)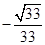 .
.
【解析】(I)可以先证明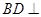 平面
平面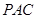 ,再证明
,再证明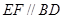 即可.
即可.
(II)连接CM,若 平面
平面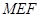 ,平面
,平面 平面
平面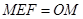 ,∴
,∴
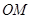 ,从而可根据平行线分线段成比例定理,可确定点M的位置.
,从而可根据平行线分线段成比例定理,可确定点M的位置.
(III)不难找出二面角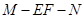 的平面角为
的平面角为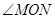 ,然后解三角形MON求角即可.
,然后解三角形MON求角即可.
(Ⅰ)连结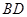 ,∵
,∵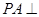 平面
平面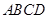 ,
,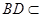 平面
平面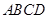 ,∴
,∴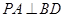 ,
,
又∵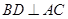 ,
,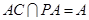 ,
,
∴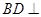 平面
平面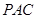 ,
,
又∵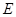 ,
, 分别是
分别是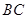 、
、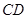 的中点,∴
的中点,∴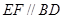 ,
,
∴ 平面
平面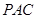 ,又
,又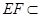 平面
平面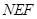 ,
,
∴平面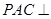 平面
平面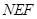 ;---------------------------------------4分
;---------------------------------------4分
(Ⅱ)连结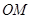 ,
,
∵ 平面
平面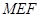 ,平面
,平面 平面
平面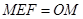 ,∴
,∴
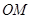 ,
,
∴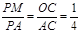 ,故
,故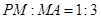 ----------------------------6分
----------------------------6分
(Ⅲ)∵ 平面
平面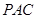 ,
, 平面
平面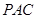 ,∴
,∴
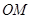 ,
,
在等腰三角形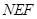 中,点
中,点 为
为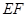 的中点,∴
的中点,∴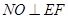 ,
,
∴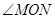 为所求二面角
为所求二面角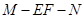 的平面角,
---------------------------------8分
的平面角,
---------------------------------8分
∵点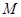 是
是 的中点,∴
的中点,∴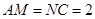 ,
,
所以在矩形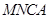 中,可求得
中,可求得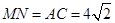 ,
, ,
,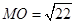 ,----------10分
,----------10分
在 中,由余弦定理可求得
中,由余弦定理可求得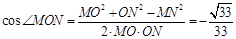 ,
,
∴二面角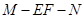 的余弦值为
的余弦值为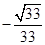 . ------------------------------12分
. ------------------------------12分

练习册系列答案
相关题目