Question

抛物线y=

1

2

x2将圆面x²+y²≤8分成两部分，现在向圆面上均匀投点，这些点落在图中阴影部分的概率为

1

4

+

1

6π

，则定积分

∫

2 0

(

8-x2

-

1

2

x2)dx=

 

．

Answer 1

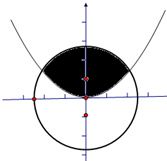
分析：先由向圆面上均匀投点，这些点落在图中阴影部分的概率为

1

4

+

1

6π

，再转化为几何概型的面积类型求解，求出阴影部分的面积，根据定积分的几何意义，求得结果．

解答：解：解方程组

x2+y2=8 y= 1 2 x2

可得到x=±2所以阴影部分的面积为积分

∫

2 -2

(

8-x2

-

1

2

x2)dx，
根据几何概型可得阴影部分的面积是2π+

4

3

，
∴

∫

2 0

(

8-x2

-

1

2

x2)dx=π+

2

3

故答案为π+

2

3

点评：本题主要考查实验法求概率以及几何概型中面积类型，以及定积分的几何意义，将两者建立关系，引入方程思想．属中档题．