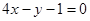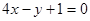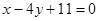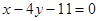题目内容
(本大题13分)已知函数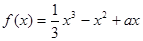 (
(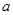 为常数)
为常数)
(1)若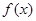 在区间
在区间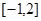 上单调递减,求
上单调递减,求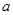 的取值范围;
的取值范围;
(2)若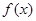 与直线
与直线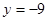 相切:
相切:
(ⅰ)求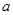 的值;
的值;
(ⅱ)设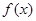 在
在 处取得极值,记点M (
处取得极值,记点M (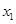 ,
,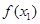 ),N(
),N(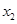 ,
,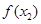 ),P(
),P(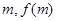 ),
), 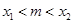 , 若对任意的m
, 若对任意的m  (
(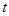 , x
, x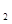 ),线段MP与曲线f(x)均有异于M,P的公共点,试确定
),线段MP与曲线f(x)均有异于M,P的公共点,试确定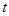 的最小值,并证明你的结论.
的最小值,并证明你的结论.
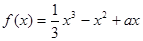 (
(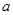 为常数)
为常数)(1)若
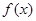 在区间
在区间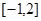 上单调递减,求
上单调递减,求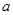 的取值范围;
的取值范围;(2)若
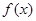 与直线
与直线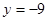 相切:
相切:(ⅰ)求
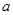 的值;
的值;(ⅱ)设
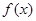 在
在 处取得极值,记点M (
处取得极值,记点M (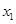 ,
,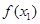 ),N(
),N(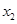 ,
,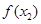 ),P(
),P(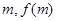 ),
), 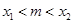 , 若对任意的m
, 若对任意的m  (
(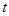 , x
, x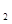 ),线段MP与曲线f(x)均有异于M,P的公共点,试确定
),线段MP与曲线f(x)均有异于M,P的公共点,试确定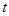 的最小值,并证明你的结论.
的最小值,并证明你的结论. (1)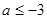 (2) (i)a=-3 , ii) 2.
(2) (i)a=-3 , ii) 2.
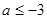 (2) (i)a=-3 , ii) 2.
(2) (i)a=-3 , ii) 2. (1)根据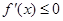 在
在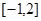 上恒成立,然后再分离常数转化为最值问题来解决.
上恒成立,然后再分离常数转化为最值问题来解决.
(2)(i)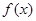 与直线
与直线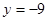 相切可知切点(x0,-9)在f(x)的图像上,并且
相切可知切点(x0,-9)在f(x)的图像上,并且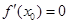 ,
,
从而可求出切点坐标,及a值.
(ii)先求出MN的坐标,进而求出MN的直线方程,然后再与y=f(x)联立消去y得到关于x的一元三次方程,说明此方程在区间[xM,xN]上有实数解,再构造函数利用导数确定其图像从而确定t的取值范围,确定出t的最小值.
(1)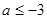 (2) (i)a=-3
(2) (i)a=-3
ii)

即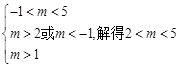
又因为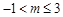 ,所以m 的取值范围为(2,3)
,所以m 的取值范围为(2,3)
又因为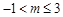 ,所以m 的取值范围为(2,3)
,所以m 的取值范围为(2,3)
从而满足题设条件的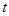 的最小值为2. ………….
的最小值为2. ………….
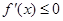 在
在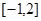 上恒成立,然后再分离常数转化为最值问题来解决.
上恒成立,然后再分离常数转化为最值问题来解决.(2)(i)
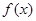 与直线
与直线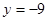 相切可知切点(x0,-9)在f(x)的图像上,并且
相切可知切点(x0,-9)在f(x)的图像上,并且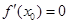 ,
,从而可求出切点坐标,及a值.
(ii)先求出MN的坐标,进而求出MN的直线方程,然后再与y=f(x)联立消去y得到关于x的一元三次方程,说明此方程在区间[xM,xN]上有实数解,再构造函数利用导数确定其图像从而确定t的取值范围,确定出t的最小值.
(1)
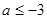 (2) (i)a=-3
(2) (i)a=-3 ii)

即
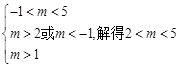
又因为
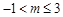 ,所以m 的取值范围为(2,3)
,所以m 的取值范围为(2,3)又因为
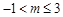 ,所以m 的取值范围为(2,3)
,所以m 的取值范围为(2,3)从而满足题设条件的
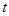 的最小值为2. ………….
的最小值为2. ………….
练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
 的导函数
的导函数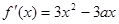 ,
,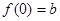 ,
,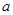 .
.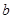 为实数.
为实数.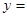
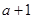 ,
,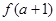 )处切线的斜率为12,求
)处切线的斜率为12,求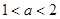 ,求函数
,求函数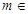 R,函数
R,函数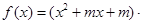 e
e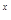 .
. 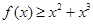 .
.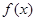 是最小正周期为
是最小正周期为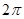 的偶函数,
的偶函数,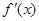 是
是 时,
时,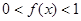 ;当
;当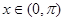 且
且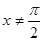 时 ,
时 ,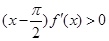 ,则函数
,则函数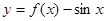 在
在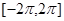 上的零点个数为( )
上的零点个数为( )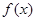 的图象在点P处的切线方程是y=-x+8,则f(5)+f’(5)=
的图象在点P处的切线方程是y=-x+8,则f(5)+f’(5)=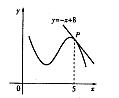
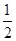
 是曲线
是曲线 在
在 处的切线,
处的切线, ,若
,若 ,则
,则 的取值范围是( )
的取值范围是( )



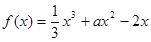 在区间
在区间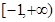 上有极大值和极小值,则实数
上有极大值和极小值,则实数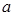 的取值范围是
的取值范围是 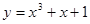 在点(1,3)处的切线方程是( )
在点(1,3)处的切线方程是( )