题目内容
设f(x)=ln(x+1)+ax,(a∈R且a≠0).
(Ⅰ)讨论函数f(x)的单调性;
(Ⅱ)若a=1,证明: 成立.
成立.
(Ⅰ)解:函数f(x)的定义域为(0,+∞),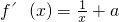
当a>0时,f′(x)>0,
∴f(x)在(0,+∞)上是增函数;
当a<0时,由f′(x)>0得 ;由f′(x)<0得
;由f′(x)<0得
∴函数f(x)在( )上是增函数,在
)上是增函数,在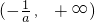 上是减函数;
上是减函数;
(Ⅱ)a=1时,f(x)=ln(x+1)+x
要证 成立,由于x>0,则只需证明xlnx+x2-3x-1<0在x∈[1,2]时恒成立.
成立,由于x>0,则只需证明xlnx+x2-3x-1<0在x∈[1,2]时恒成立.
令g(x)=xlnx+x2-3x-1,则g′(x)=lnx+2x-2
设h(x)=lnx+2x-2,则∵x∈[1,2],∴
∴函数h(x)在x∈[1,2]时单调递增
∵h(1)=0,∴g′(x)≥0
∴函数g(x)在x∈[1,2]时单调递增
∴g(x)≤g(2)=2ln2-3<0
∴xlnx+x2-3x-1<0在x∈[1,2]时恒成立
∴ 成立.
成立.
分析:(Ⅰ)确定函数f(x)的定义域,求导函数,分类讨论,利用导数的正负,可得函数的单调区间;
(Ⅱ)要证 成立,由于x>0,则只需证明xlnx+x2-3x-1<0在x∈[1,2]时恒成立,构造函数,确定函数的单调性,即可得证.
成立,由于x>0,则只需证明xlnx+x2-3x-1<0在x∈[1,2]时恒成立,构造函数,确定函数的单调性,即可得证.
点评:本题考查导数知识的运用,考查函数的单调性,考查分类讨论的数学思想,考查不等式的证明,确定函数的单调性是关键.
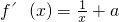
当a>0时,f′(x)>0,
∴f(x)在(0,+∞)上是增函数;
当a<0时,由f′(x)>0得
 ;由f′(x)<0得
;由f′(x)<0得
∴函数f(x)在(
 )上是增函数,在
)上是增函数,在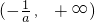 上是减函数;
上是减函数;(Ⅱ)a=1时,f(x)=ln(x+1)+x
要证
 成立,由于x>0,则只需证明xlnx+x2-3x-1<0在x∈[1,2]时恒成立.
成立,由于x>0,则只需证明xlnx+x2-3x-1<0在x∈[1,2]时恒成立.令g(x)=xlnx+x2-3x-1,则g′(x)=lnx+2x-2
设h(x)=lnx+2x-2,则∵x∈[1,2],∴

∴函数h(x)在x∈[1,2]时单调递增
∵h(1)=0,∴g′(x)≥0
∴函数g(x)在x∈[1,2]时单调递增
∴g(x)≤g(2)=2ln2-3<0
∴xlnx+x2-3x-1<0在x∈[1,2]时恒成立
∴
 成立.
成立.分析:(Ⅰ)确定函数f(x)的定义域,求导函数,分类讨论,利用导数的正负,可得函数的单调区间;
(Ⅱ)要证
 成立,由于x>0,则只需证明xlnx+x2-3x-1<0在x∈[1,2]时恒成立,构造函数,确定函数的单调性,即可得证.
成立,由于x>0,则只需证明xlnx+x2-3x-1<0在x∈[1,2]时恒成立,构造函数,确定函数的单调性,即可得证.点评:本题考查导数知识的运用,考查函数的单调性,考查分类讨论的数学思想,考查不等式的证明,确定函数的单调性是关键.

练习册系列答案
相关题目