题目内容
在等差数列{an}中,a1=3,其前n项和为Sn,等比数列{bn}的各项均为正数,b1=1,公比为q,且b2+S2=12,![]() .
.
(Ⅰ)求an与bn;
(Ⅱ)设cn=an•bn,求数列{cn}的前n项和Tn.
考点:
等比数列的通项公式;等差数列的通项公式;数列的求和.
专题:
综合题;等差数列与等比数列.
分析:
(1)根据b2+S2=12,{bn}的公比![]() ,建立方程组,即可求出an与bn;
,建立方程组,即可求出an与bn;
(2)由an=3n,bn=3n﹣1,知cn=an•bn=n•3n,由此利用错位相减法能求出数列{cn}的前n项和Tn.
解答:
解:(1)∵在等差数列{an}中,a1=3,其前n项和为Sn,
等比数列{bn}的各项均为正数,b1=1,公比为q,且b2+S2=12,![]() .
.
∴b2=b1q=q,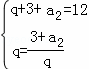 ,(3分)
,(3分)
解方程组得,q=3或q=﹣4(舍去),a2=6(5分)
∴an=3+3(n﹣1)=3n,bn=3n﹣1.(7分)
(2)∵an=3n,bn=3n﹣1,
∴cn=an•bn=n•3n,
∴数列{cn}的前n项和
Tn=1×3+2×32+3×33+…+n×3n,
∴3Tn=1×32+2×33+3×34+…+n×3n+1,
∴﹣2Tn=3+32+33+…+3n﹣n×3n+1
=![]() ﹣n×3n+1
﹣n×3n+1
=![]() ﹣n×3n+1,
﹣n×3n+1,
∴Tn=![]() ×3n+1﹣
×3n+1﹣![]() .
.
点评:
本题考查数列的通项公式和前n项和公式的求法,解题时要认真审题,注意等差数列、等比数列的性质和错位相减法的合理运用.

练习册系列答案
相关题目