题目内容
已知函数f(x)=(1)证明函数f(x)在定义域上有反函数,并求出反函数;
(2)反函数的图象与直线y=x有无交点?
(1)证明:∵f(x)的定义域为正实数集,
∴当0<x1<x2时,f(x1)-f(x2)=(![]() )-(
)-(![]() )=(
)=(![]() )(1+
)(1+![]() )<0.
)<0.
∴f(x1)<f(x2),即f(x)在(0,+∞)上是增函数.
∴f(x)有反函数.当x∈(0,+∞)时,![]() ∈(-∞,+∞).∴反函数的定义域为R.
∈(-∞,+∞).∴反函数的定义域为R.
由y=![]() ,得x-y
,得x-y![]() -1=0.
-1=0.
解得![]() =
=![]() .∵y<
.∵y<![]() ,
,
∴y-![]() <0.而
<0.而![]() >0,
>0,
∴![]() =
=![]() ,x=
,x=![]() (y+
(y+![]() )2.
)2.
∴f-1(x)=![]() (x+
(x+![]() )2(x∈R).
)2(x∈R).
(2)解:y=f-1(x)与y=f(x)的图象关于y=x对称,故只需判断y=f(x)与y=x有无交点.
由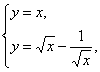 得x=
得x=![]() .
.
∴x(1-![]() )=1.
)=1.
当0<x<1时,0<1-![]() <1.∴0<x(1-
<1.∴0<x(1-![]() )<1,此时方程无实数根.
)<1,此时方程无实数根.
当x≥1时,x(1-![]() )≤0,方程无实根.
)≤0,方程无实根.
∴y=f(x)与y=x无交点.
从而y=f-1(x)与y=x无交点.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 已知函数f(x)=
已知函数f(x)=
|
A、(
| ||||
B、(
| ||||
C、(
| ||||
D、[
|