Question

已知p:{x|}；q：{x|1-m≤x≤1+m,m＞0}，若p是q的必要不充分条件，求实数m的取值范围.

Answer 1

解析：先写出p和q，然后由qp但p q，求得m的范围.

解法一：p即{x|-2≤x≤10},所以p：A={x|x＜-2或x＞10},q：B={x|x＜1-m或x＞1+m,m＞0}.

因为p是q的必要不充分条件，

所以qp,p q,

所以BA，画数轴分析知，BA的充要条件是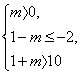或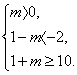

解得m≥9，即m的取值范围是{m|m≥9}.

解法二：因为p是q的必要不充分条件，即qp,所以pq，所以p是q的充分不必要条件.

而p：P={x|-2≤x≤10}.

q：Q={x|1-m≤x≤1+m,m＞0}.

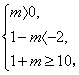所以PQ，即得或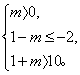解得m≥9.

所以m的取值范围是{m|m≥9}.

点评：解法一是直接利用必要不充分条件和集合包含关系得出m的不等式组；解法二是利用命题等价关系，得出p是q的充分不必要条件，不需要求p、q对应的集合.本题易错在地方是解不等式组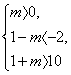m＞9.漏解m=9，请认真体会原因.