题目内容
给出下列命题:①不等式|x-lgx|<x+|lgx|成立的充要条件是x>1;
②已知函数
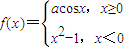 在x=0处连续,则a=-1;
在x=0处连续,则a=-1;③当x∈[0,1]时,不等式
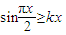 恒成立,则实数k的取值范围是[0,1];
恒成立,则实数k的取值范围是[0,1];④将函数
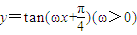 的图象按向量
的图象按向量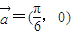 平移后,与函数
平移后,与函数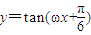 的图象重合,则ω的最小值为
的图象重合,则ω的最小值为 .
.你认为正确的命题是 .(写出所有正确命题的序号)
【答案】分析:①不等式|x-lgx|<x+|lgx|?|x-lgx|2<(x+|lgx|)2?2x(lgx+|lgx|)>0?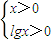 ,从而可判断①的正误;
,从而可判断①的正误;
②利用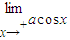 =a=
=a=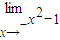 =-1,可判断②的正误;
=-1,可判断②的正误;
③可令x= ,k=
,k=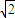 ,有
,有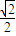 ≥
≥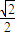 ,成立,从而可③的正判断误;
,成立,从而可③的正判断误;
④ y=tan(ω(x-
y=tan(ω(x-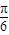 )+
)+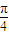 )=tan(ωx+
)=tan(ωx+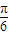 )?ω=
)?ω= -6k(k∈Z),由此可判断④的正误;
-6k(k∈Z),由此可判断④的正误;
解答:解:∵|x-lgx|<x+|lgx|?|x-lgx|2<(x+|lgx|)2?2x(lgx+|lgx|)>0? ?x>1,
?x>1,
∴①正确;
∵函数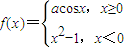 在x=0处连续,
在x=0处连续,
∴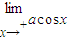 =a=
=a= =-1,
=-1,
∴a=-1,即②正确;
在③中,不妨令x= ,k=
,k=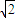 ,有
,有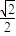 ≥
≥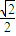 ,成立,故实数k的取值范围是[0,1]是错误的;
,成立,故实数k的取值范围是[0,1]是错误的;
在④中, y=tan(ω(x-
y=tan(ω(x-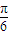 )+
)+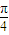 )=tan(ωx+
)=tan(ωx+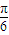 )?ω=
)?ω= -6k(k∈Z),
-6k(k∈Z),
令k=0,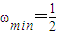 由此可判断④是错误的;
由此可判断④是错误的;
故答案为:①②
点评:本题考查充要条件,函数的连续性的概念,正切函数的图象,正弦函数的图象,难点在于充要条件问题的合理的转化、恒成立问题的灵活与综合应用,属于难题
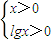 ,从而可判断①的正误;
,从而可判断①的正误;②利用
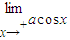 =a=
=a=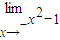 =-1,可判断②的正误;
=-1,可判断②的正误;③可令x=
 ,k=
,k=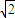 ,有
,有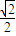 ≥
≥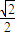 ,成立,从而可③的正判断误;
,成立,从而可③的正判断误;④
 y=tan(ω(x-
y=tan(ω(x-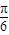 )+
)+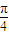 )=tan(ωx+
)=tan(ωx+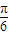 )?ω=
)?ω= -6k(k∈Z),由此可判断④的正误;
-6k(k∈Z),由此可判断④的正误;解答:解:∵|x-lgx|<x+|lgx|?|x-lgx|2<(x+|lgx|)2?2x(lgx+|lgx|)>0?
 ?x>1,
?x>1,∴①正确;
∵函数
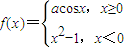 在x=0处连续,
在x=0处连续,∴
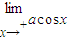 =a=
=a= =-1,
=-1,∴a=-1,即②正确;
在③中,不妨令x=
 ,k=
,k=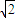 ,有
,有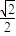 ≥
≥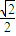 ,成立,故实数k的取值范围是[0,1]是错误的;
,成立,故实数k的取值范围是[0,1]是错误的;在④中,
 y=tan(ω(x-
y=tan(ω(x-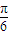 )+
)+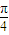 )=tan(ωx+
)=tan(ωx+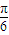 )?ω=
)?ω= -6k(k∈Z),
-6k(k∈Z),令k=0,
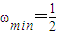 由此可判断④是错误的;
由此可判断④是错误的;故答案为:①②
点评:本题考查充要条件,函数的连续性的概念,正切函数的图象,正弦函数的图象,难点在于充要条件问题的合理的转化、恒成立问题的灵活与综合应用,属于难题

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
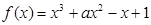 ,给出下列命题:
,给出下列命题: =0一定有三个不等的实数根.
=0一定有三个不等的实数根.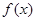 =x3+ax2-x+1,给出下列命题:
=x3+ax2-x+1,给出下列命题: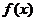 =x3+ax2-x+1,给出下列命题:
=x3+ax2-x+1,给出下列命题: