题目内容
已知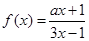 ,且方程
,且方程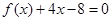 有两个不同的正根,其中一根是另一根的
有两个不同的正根,其中一根是另一根的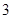 倍,记等差数列
倍,记等差数列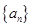 、
、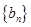 的前
的前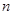 项和分别为
项和分别为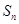 ,
,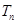 且
且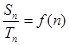 (
(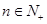 )。
)。
(1)若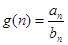 ,求
,求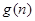 的最大值;
的最大值;
(2)若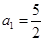 ,数列
,数列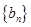 的公差为3,试问在数列
的公差为3,试问在数列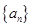 与
与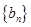 中是否存在相等的项,若存在,求出由这些相等项从小到大排列得到的数列
中是否存在相等的项,若存在,求出由这些相等项从小到大排列得到的数列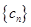 的通项公式;若不存在,请说明理由.
的通项公式;若不存在,请说明理由.
(3)若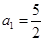 ,数列
,数列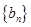 的公差为3,且
的公差为3,且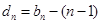 ,
,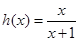 .
.
试证明: .
.
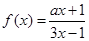 ,且方程
,且方程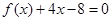 有两个不同的正根,其中一根是另一根的
有两个不同的正根,其中一根是另一根的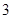 倍,记等差数列
倍,记等差数列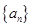 、
、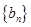 的前
的前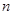 项和分别为
项和分别为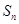 ,
,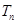 且
且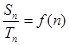 (
(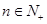 )。
)。(1)若
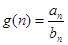 ,求
,求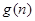 的最大值;
的最大值;(2)若
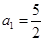 ,数列
,数列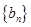 的公差为3,试问在数列
的公差为3,试问在数列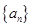 与
与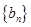 中是否存在相等的项,若存在,求出由这些相等项从小到大排列得到的数列
中是否存在相等的项,若存在,求出由这些相等项从小到大排列得到的数列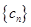 的通项公式;若不存在,请说明理由.
的通项公式;若不存在,请说明理由.(3)若
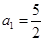 ,数列
,数列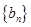 的公差为3,且
的公差为3,且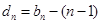 ,
,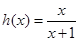 .
.试证明:
 .
.(1) (2)在数列
(2)在数列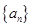 与
与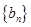 中不存在相等的项。
中不存在相等的项。
(3)运用数序归纳法来证明与自然数相关的命题得到结论。
 (2)在数列
(2)在数列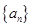 与
与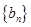 中不存在相等的项。
中不存在相等的项。(3)运用数序归纳法来证明与自然数相关的命题得到结论。
试题分析:解:(1)
 ,
, ,
,
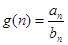
 故
故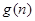 的最大值为
的最大值为 。
。(2)由(1)知
 ,
, 可得
可得 ,
,
令
 ,
, 可得:
可得: 矛盾
矛盾所以在数列
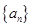 与
与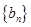 中不存在相等的项。
中不存在相等的项。(3)证明:∵
 ∴要证
∴要证
即要证
 (直接用数学归纳法证明不出)
(直接用数学归纳法证明不出)只要证明
 (再用数学归纳法证明即可)
(再用数学归纳法证明即可)提示:当
 时,只要证:
时,只要证:


点评:主要是考查了数列与不等式以及数列的性质的运用,属于难度题。

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案 走进文言文系列答案
走进文言文系列答案
相关题目
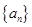 是等差数列,若
是等差数列,若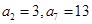 ,则数列
,则数列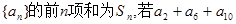 为一个确定的常数,则下列各个前
为一个确定的常数,则下列各个前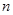 项和中,也为确定的常数的是 ( )
项和中,也为确定的常数的是 ( )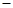 3n+1
3n+1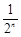
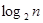
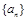 和公比为
和公比为
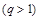 的等比数列
的等比数列 满足:
满足: ,
, ,
,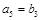 .
. 的前
的前 项和为
项和为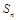 .
. }的前n项和
}的前n项和 ,数列{
,数列{ }满足
}满足 .
. ,数列
,数列 的前
的前 项和为
项和为 ,求满足
,求满足 的
的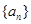 的前
的前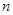 项和为
项和为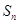 .若
.若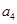 是
是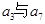 的等比中项,
的等比中项, 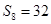 ,则
,则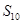 等于()
等于() 中
中 等差数列且
等差数列且 ,若
,若 则
则
 中,
中, ,那么
,那么 等于 .
等于 .