题目内容
已知命题p:?x∈R,使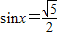 ;命题q:?x∈R,都有x2+x+1>0.给出下列结论:
;命题q:?x∈R,都有x2+x+1>0.给出下列结论:①命题“p∧q”是真命题;
②命题“p∧¬q”是假命题;
③命题“¬p∨q”是真命题;
④命题“¬p∨¬q”是假命题.
其中正确的是( )
A.②③
B.②④
C.③④
D.①②③
【答案】分析:根据正弦函数的值域及二次不等式的解法,我们易判断命题p:?x∈R,使sin x=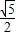 与命题q:?x∈R,都有x2+x+1>0的真假,进而根据复合命题的真值表,易判断四个结论的真假,最后得到结论.
与命题q:?x∈R,都有x2+x+1>0的真假,进而根据复合命题的真值表,易判断四个结论的真假,最后得到结论.
解答:解:∵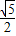 >1,结合正弦函数的性质,易得命题p:?x∈R,使sin x=
>1,结合正弦函数的性质,易得命题p:?x∈R,使sin x=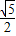 为假命题,
为假命题,
又∵x2+x+1=(x+ )2+
)2+ >0恒成立,∴q为真命题,故非p是真命题,非q是假命题;
>0恒成立,∴q为真命题,故非p是真命题,非q是假命题;
所以①p∧q是假命题,错;
②p∧非q是假命题,正确;
③非p∨q是真命题,正确;
④命题“¬p∨¬q”是假命题,错;
故答案为:②③
故选A.
点评:本题考查的知识点是复合命题的真假,其中根据正弦函数的值域及二次不等式的解法,判断命题p与命题q的真假是解答的关键.
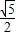 与命题q:?x∈R,都有x2+x+1>0的真假,进而根据复合命题的真值表,易判断四个结论的真假,最后得到结论.
与命题q:?x∈R,都有x2+x+1>0的真假,进而根据复合命题的真值表,易判断四个结论的真假,最后得到结论.解答:解:∵
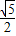 >1,结合正弦函数的性质,易得命题p:?x∈R,使sin x=
>1,结合正弦函数的性质,易得命题p:?x∈R,使sin x=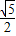 为假命题,
为假命题,又∵x2+x+1=(x+
 )2+
)2+ >0恒成立,∴q为真命题,故非p是真命题,非q是假命题;
>0恒成立,∴q为真命题,故非p是真命题,非q是假命题;所以①p∧q是假命题,错;
②p∧非q是假命题,正确;
③非p∨q是真命题,正确;
④命题“¬p∨¬q”是假命题,错;
故答案为:②③
故选A.
点评:本题考查的知识点是复合命题的真假,其中根据正弦函数的值域及二次不等式的解法,判断命题p与命题q的真假是解答的关键.

练习册系列答案
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目