题目内容
已知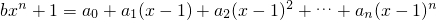
对任意x∈R恒成立，且a1=9，a2=36，则b=
- A.1
- B.2
- C.3
- D.4
A
分析：根据 bxn+1=b[1+（x-1）]n+1，根据它的展开式形式，由题意可得 b
=9，b
=36，由此求出b的值．
解答：∵bxn+1=b[1+（x-1）]n+1=
，且a1=9，a2=36，
∴b=9，b=36，解得 b=1，n=9，
故选A．
点评：本题主要考查二项式定理的应用，二项展开式的通项公式，求展开式中某项的系数，属于中档题．
分析：根据 bxn+1=b[1+（x-1）]n+1，根据它的展开式形式，由题意可得 b
=9，b=36，由此求出b的值．解答：∵bxn+1=b[1+（x-1）]n+1=
，且a1=9，a2=36，∴b
=9，b=36，解得 b=1，n=9，故选A．
点评：本题主要考查二项式定理的应用，二项展开式的通项公式，求展开式中某项的系数，属于中档题．
练习册系列答案
相关题目