题目内容
(本小题满分12分)已知A、B、C为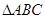 的三个内角且向量
的三个内角且向量
 共线。
共线。
(Ⅰ)求角C的大小:
(Ⅱ)设角 的对边分别是
的对边分别是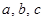 ,且满足
,且满足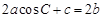 ,试判断
,试判断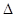
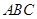 的形状.
的形状.
【答案】
(1) (2)△
(2)△ 为等边三角形
为等边三角形
【解析】
试题分析:(Ⅰ)(Ⅰ)∵ 与
与 共线
共线
∴
 …………………………3分
…………………………3分
得 …………………………4分
…………………………4分
∴C= ……………………………6分
……………………………6分
(Ⅱ)方法1:由已知 (1)
(1)
根据余弦定理可得: (2)……………………8分
(2)……………………8分
(1)、(2)联立解得: ……………………………10分
……………………………10分
 为等边三角形,……………………………12分
为等边三角形,……………………………12分
方法2:
由正弦定理得:
 ……………………8分
……………………8分
∴ , ∴在△
, ∴在△ 中 ∠
中 ∠ . ……………………………10分
. ……………………………10分
 为等边三角形 ……………………………12分
为等边三角形 ……………………………12分
方法3:由(Ⅰ)知C= ,又由题设得:
,又由题设得: ,
,
在 中根据射影定理得:
中根据射影定理得:
 ……………………8分
……………………8分
 ……………………………10分
……………………………10分
又. C= , 所以 △
, 所以 △ 为等边三角形, ……………………………12分
为等边三角形, ……………………………12分
考点:考查了解三角形运用。
点评:解决该试题的关键是对于向量共线以及两角和差的三角关系式的变形求解,同时能结合三角形的两个定理来确定形状,属于基础题。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目