题目内容
两千多年前,古希腊毕达哥拉斯学派的数学家曾经在沙滩上研究数学问题,他们在沙滩上画点或用小石子来表示数,按照点或小石子能排列的形状对数进行分类,如图2中的实心点个数1,5,12,22,…,被称为五角形数,其中第1个五角形数记作 ,第2个五角形数记作
,第2个五角形数记作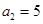 ,第3个五角形数记作
,第3个五角形数记作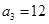 ,第4个五角形数记作
,第4个五角形数记作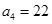 ,…,若按此规律继续下去,得数列
,…,若按此规律继续下去,得数列 ,则
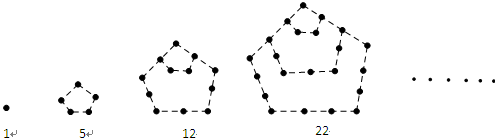
,则 ;对
;对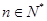 ,
,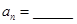 .
.
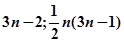
解析试题分析:因为 ,
,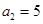 ,
,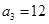 ,
,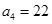 …………
…………
所以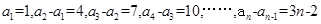
以上n个式子相加,得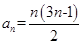 。
。
考点:数列的应用;数列通项公式的求法。
点评:做这类题目最重要的就是寻找规律。此题通过寻找前一项与后一项差的规律,进而求出数列 的通项公式。
的通项公式。

练习册系列答案
 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目
数列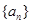 的前
的前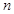 项和为
项和为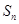 ,若
,若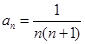 ,则
,则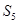 等于( )
等于( )
| A.1 | B.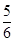 | C.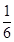 | D.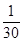 |
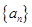 的通项为
的通项为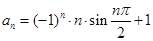 前
前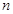 项和为
项和为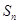 , 则
, 则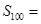 _________.
_________.
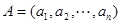 ,
,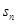 为其前n项和,定义
为其前n项和,定义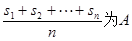 的“凯森和”,若有99项的数列
的“凯森和”,若有99项的数列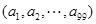 的“凯森和”为1000,则有100项的数列
的“凯森和”为1000,则有100项的数列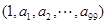 的“凯森和”为 .
的“凯森和”为 .
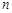 个“金鱼”图需要火柴棒的根数为_________.
个“金鱼”图需要火柴棒的根数为_________.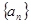 的前
的前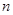 项和
项和 ,则
,则 ________________;
________________;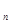 }满足0<a
}满足0<a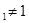 , 且
, 且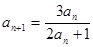 (n
(n N*).
N*). 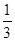 ,求出a2、a3、a4、a5的值,归纳出an , 并用数学归纳法证明.
,求出a2、a3、a4、a5的值,归纳出an , 并用数学归纳法证明.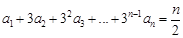 ,则
,则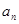 = .
= .